No artigo anterior, vimos sobre as diferentes Estruturas de Dados que são utilizadas para distribuir e relacionar os dados, de modo a tornar os algoritmos, que manipulam esses dados, mais eficientes. Porém, como medir o quanto nossos algoritmos são eficientes?
Quando pensamos em algoritmos, logo vem à mente um procedimento onde pode haver entradas em uma sequência de passos e operações para produzir uma saída que satisfaça a resolução de um problema. Segundo Cormen (2002), um algoritmo é qualquer procedimento computacional bem definido que toma algum valor ou conjunto de valores como entrada e produz algum valor ou conjunto de valores como saída. Esta afirmação está congruente a nossa linha de pensamento. Para um algoritmo ser satisfatório, temos que conseguir avaliá-lo para saber se ele atende ou não as nossas expectativas. Simplesmente produzir uma saída qualquer, pode não ser satisfatório. Imagine um algoritmo simples que efetue uma operação básica de soma, exemplo 20 + 3 + 15, e demora-se 5 minutos para retornar um resultado, esse algoritmo é considerado bom? É satisfatório?
Fica claro que temos que avaliar as entradas, o processamento e a saída. As entradas são as instâncias do problema e é sobre essas instâncias que temos que nos preocupar na hora de implementarmos nossos algoritmos. Por exemplo, imagine um algoritmo que recebe como entrada uma estrutura de dados e gera a ordenação de seus elementos, dizemos que o Input representa a instância do problema, a finalidade do algoritmo define o que será solucionado e o Output o resultado esperado.
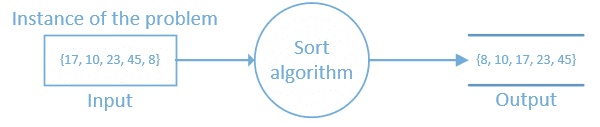
É sobre essa ótica que você vai analisar a complexidade do algoritmo com vista no tamanho do problema. Diferentes computadores, muitas vezes com hardwares idênticos, podem levar tempos diferentes para processar um mesmo algoritmo. Por tanto, avaliar o desempenho de um algoritmo com base apenas no tempo de execução deste, é ineficiente.
Quando estudamos a complexidade de um algoritmo, estamos definindo quão eficiente ele é em relação ao número de operações (passos) necessárias para sua conclusão. A preocupação principal se dá quando temos que processar uma quantidade alta de dados. E é através da análise assintótica que conseguimos analisar o comportamento de um algoritmo tendo em vista esse grande volume de dados de entrada.
Para medir a complexidade de um algoritmo utilizamos uma função de complexidade f , onde f(n) é a medida do tempo/espaço necessário para executar um algoritmo para um problema de tamanho n, ou seja, com a função de complexidade de tempo podemos medir o número de operações necessárias para executar um algoritmo e a complexidade de espaço medimos a memória necessária para a execução de um algoritmo. Ao relacionarmos o número de instruções com o tamanho do conjunto de dados podemos ter 3 possíveis cenários: melhor caso, caso médio e o pior caso.
O melhor caso corresponde ao menor tempo de execução sobre todas as possíveis entradas de tamanho n, f(n) = Ω(1)
O caso médio corresponde à média dos tempos de execução de todas as entradas de tamanho n, f(n) = θ(n/2)
O pior caso corresponde ao maior tempo de execução sobre todas as entradas de tamanho n, f(n) = O(n)
Note que utilizamos 3 notações para representar os possíveis casos: Ômega (Ω), Theta(θ) e Ômicron (Big O). A maneira mais comum de analisar um algoritmo é pelo pior caso, Big O. Você naturalmente não avalia o melhor caso, porque essas condições não são atingidas com frequência.
Conceitualmente funciona assim: Se um tempo de execução é O(f(n)), então para um n suficientemente grande, o tempo de execução é no máximo c*f(n) para alguma constante c, onde c > 0. Dizemos que o tempo de execução é big-O de f(n) ou simplesmente O de f(n).
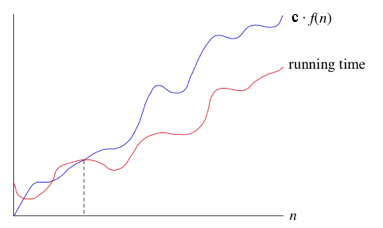
Outra forma mais usual de representar é dizer que f(n) = O(g(n)). Quando dizemos que f(n) = O(g(n)) garantimos que g(n) é um limite superior sobre f(n). Escrito desta forma: f(n) ≤ c · g(n), onde c é uma constante positiva, como dito anteriormente.
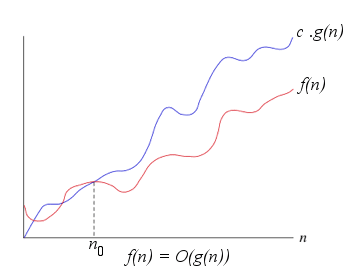
A complexidade de tempo não representa tempo diretamente, mas o número de vezes que determinada operação considerada relevante é executada. Deste modo observamos o maior peso relevante para determinar a complexidade. Por exemplo, um algoritmo para capturar o maior valor de um array de inteiros A[1..n], n ≥ 1, logo f(n) = n−1, para n ≥ 1, ou seja, possuem complexidade linear no tamanho da entrada, ou O(n), em que n é o tamanho da entrada.

Outro exemplo, ao analisarmos o algoritmo para ordenação por flutuação bubble sort, a ideia é percorrer o array diversas vezes, e a cada passagem fazer flutuar para o topo o maior elemento da sequência. No pior caso, são feitas n2 operações. A complexidade desse algoritmo é de ordem quadrática, ou O(n2)

O pior caso ocorre quando o array está ordenado em ordem decrescente, pois o algoritmo irá realizar a troca em todas as iterações. A quantidade de iterações do laço do primeiro for é igual a n-1, já o segundo laço será executado de acordo com o valor de i do primeiro for. Algo mais ou menos assim:

A resolução se dá por:
A resolução se dá por:
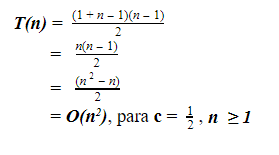
Repetindo, a notação Big O é a mais utilizada na análise de complexidade de algoritmos em geral, normalmente para pior caso, entretanto, há casos como o algoritmo QuickSort, por exemplo, que a notação O também é utilizada para o caso médio. As outras são raramente utilizadas: a notação Ω é usada algumas vezes para definição de limites inferiores. Porém, é importante lembrar que as definições de notações são independentes da análise de algoritmos, podendo ser utilizados para outros fins.
Ao comparar dois algoritmos para medir a sua eficiência, o algoritmo mais eficiente (mais rápido) será aquele cuja função de complexidade cresce mais lentamente à medida em que aumentamos o tamanho da sua entrada. As complexidades assintóticas mais comuns são:
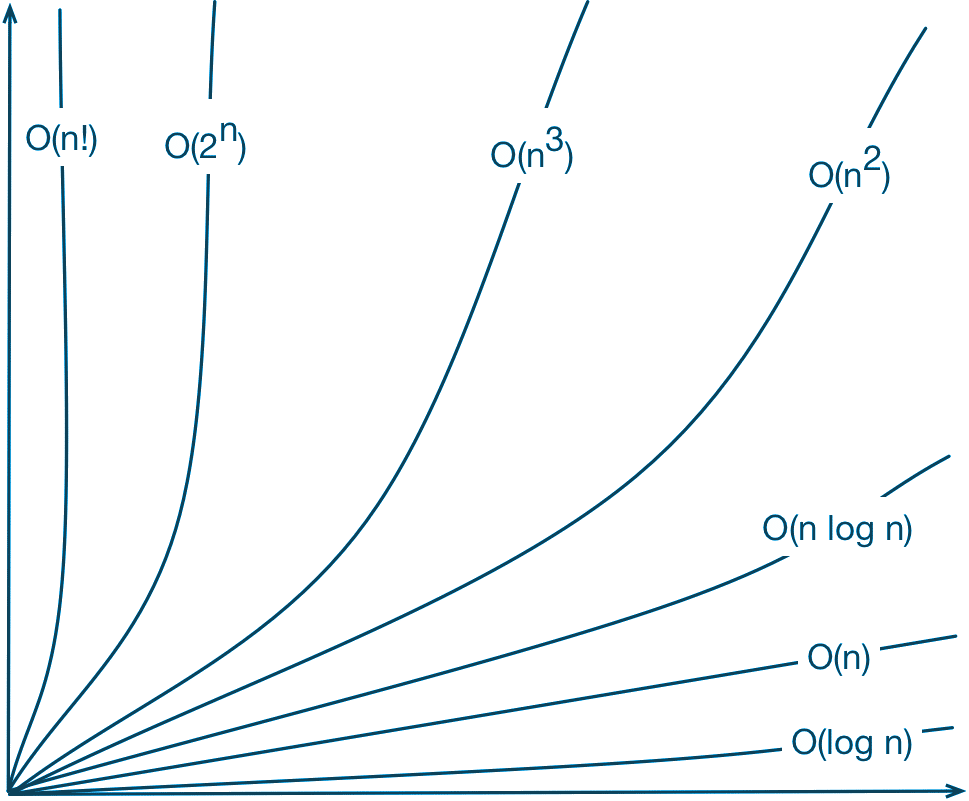
- O(1) = Complexidade constante o tempo de execução do algoritmo independe do tamanho da entrada é bem rápido.
- O(log(n)) = Complexidade logarítmica o tempo de execução pode ser considerado menor do que uma constante grande. É super rápido
- O(n) = Complexidade linear o algoritmo realiza um número fixo de operações sobre cada elemento da entrada
- O(n log(n)) = Típico de algoritmos que dividem um problema em subproblemas, resolve cada subproblema de forma independente, e depois combina os resultados
- O(n2) = Complexidade quadrática. Típico de algoritmos que operam sobre pares dos elementos de entrada
- O(n3) = Complexidade cúbica que é útil para resolver problemas pequenos como multiplicação de matrizes
- O(2n) = Complexidade exponencial. Típicos de algoritmos que fazem busca exaustiva (força bruta) para resolver um problema
- O(n!) = Complexidade fatorial. É normalmente encontrado ao analisar a complexidade de algoritmos de força bruta, que tentam todas as possibilidades para problemas de otimização combinatória.
A entrada dos dados, como já mencionei e faço questão de repetir para você fixar, é um fator de extrema importância no que tange a análise assintótica. A análise é “input bound”, a entrada influenciará diretamente no resultado. Para você perceber com maior ênfase, veja a simulação a seguir distribuída no grid. Note que a medida que aumentamos o valor de n, impacta diretamente no consumo, é necessária uma utilização maior de recursos no algoritmo:
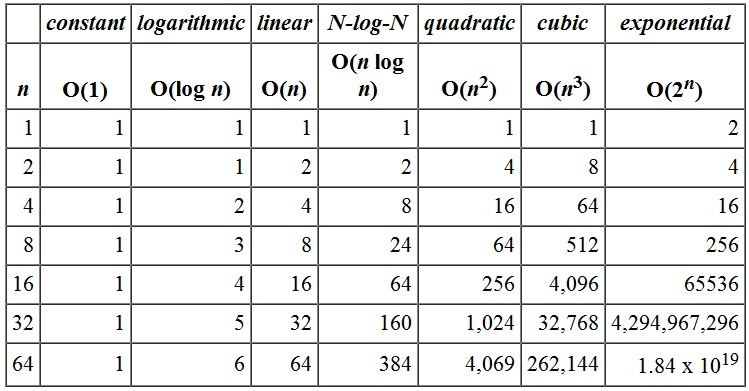
Este assunto é muito mais abrangente do que o disposto neste artigo. Para uma maior profundidade, recomendo a leitura do livro Algoritmos Teoria e Prática de Thomas Cormen (Não estou ganhando nada para divulgar esse livro, ok kkkk?)
O objetivo principal deste artigo é demonstrar a necessidade de utilizarmos técnicas de medições de complexidade dos nossos algoritmos de modo a buscarmos sempre a construção de algoritmos eficientes não apenas eficazes. A diferença entre eficácia e eficiência é que enquanto a eficácia refere-se a fazer a tarefa certa, completar atividades e alcançar metas, a eficiência é sobre fazer as coisas de forma otimizada, de maneira mais rápida ou com menos gastos. Espero que você faça bom proveito e leia e releia quantas vezes for necessário. Até o próximo artigo!
Confiança Sempre!!!
Referências:
- P. Feofiloff, Minicurso de Análise de Algoritmos, 2009.
- T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein, Introduction to Algorithms, 3rd edition, MIT Press, 2009.
- T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein, Introduction to Algorithms, 2nd edition, MIT Press & McGraw-Hill, 2001.
- Jon Kleinberg, Éva Tardos, Algorithm Design, Addison-Wesley, 2005.
- S. Dasgupta, C.H. Papadimitriou, U.V. Vazirani, Algorithms, McGraw-Hill, 2006
- G. Brassard, P. Bratley, Fundamentals of Algorithmics, Prentice Hall, 1996.
- Kurt Mehlhorn, Peter Sanders, Algorithms and Data Structures – The Basic Toolbox, Springer, 2008
- Steven Skiena, The Algorithm Design Manual, Telos/Springer-Verlag, 1998.


gostei demais, parabens
Muito obrigado Agnaldo!
Parabéns, estudo muito esse assunto, que considero um dos pilares mais importantes na área de desenvolvimento.
Ótima didática!
Muito Obrigado Diego!
Realmente, esse é um tema importantíssimo.
Acredito que todos os programadores/analistas deveriam conhecer ao menos a base, para termos profissionais cada vez mais capazes de elevar essa área para um patamar ainda maior em nosso país.