Sistema de numeração: Binário, Octal, Decimal e Hexadecimal

Atualizado pela última vez em 31 de janeiro de 2024

Já falamos diversas vezes sobre temos o uso de  abstração em grande parte do nosso dia a dia. Estamos constantemente fazendo abstração inconscientemente e você pode observar que um número é um conceito abstrato que representa a ideia de quantidade de algo.

Podemos simplificar dizendo que um Sistema de Numeração é uma forma de organizar e representar números. Existem vários tipos de sistemas, os mais comuns em informática são:

• Sistema Binário;
• Sistema Octal;
• Sistema Decimal e;
• Sistema Hexadecimal.

Sistema de numeração Decimal

Já estamos acostumados como o Sistema Decimal, onde utilizamos os símbolos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 para representar  os números. Chamamos esse sistema de base 10 porque ele utiliza 10 símbolos diferentes para representar todos os números. Vou te mostrar porque é chamado de base 10. Imagine o número 347. Fazendo uma abstração, esse número tem uma estrutura oculta de centena, dezena e unidade. Para gera esse número, o que acontece por baixo dos panos é algo assim: 

1. Primeiro pegamos 3 x 100 = 300, 
2. depois pegamos 4 x 10 = 40 e 
3. por fim 7 x 1 = 7,  onde somando tudo gera o número 347. 

Agora veja que interessante. Utilizando a base 10, a representação é a mesma, veja:

1. Fazemos 3 x 10² = 300,
2. Depois 4 x 10¹ = 40
3. e por fim 7 X 10⁰ = 7 Lembrando que 10⁰ = 1

Observe que na base 10, os expoentes vão seguindo de forma decrescente (2, 1 e 0). Se fosse um número 2347? Segue a mesma regra:

1. Fazemos 2 x 10³ = 1000, para quem não lembra 10³ = 10 x 10 x 10.
2. Na sequência 3 x 10² = 300,
3. Depois 4 x 10¹ = 40
4. e por fim 7 X 10⁰ = 7

Sistema Binário

Você deve estar pensando, utilizei os números decimais e nunca imaginei que fosse assim com esse negócio de base 10, não é? kkkkk No sistema binário, é base 2 porque você só tem o Zero (0) e o um (1) para fazer as combinações para representar os valores. Como usa apenas os símbolos 0 e 1, é mais fácil de ser representado por circuitos eletrônicos, como já explicamos em artigos anteriores.

Para você compreender como esse sistema funciona, vamos pegar o número decimal 10 e transformar em Binário. A regra é a seguinte: você vai dividindo o número por 2, separando sempre o seu resto e continuando a dividir o seu quociente até que ele seja menor que 2. Aí você pega os restos dessas divisões por 2, de baixo para cima (do último para o primeiro). Esse conjunto de retos em zeros e uns, vão compor a representação em binário. Veja o exemplo:

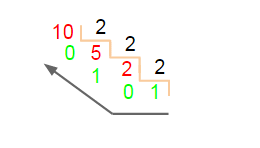
Pegando os restos da divisão de baixo para cima, temos o binário 1010. Ou seja, 10 em decimal é o mesmo que 1010 em binário. Sacou?

Existe uma segunda forma de fazermos essa conversão. Vamos agora pegar um  número maior, vamos pegar o 347 em decimal e transformar também em binário. Primeiro, vamos fazer uma tabela até o 16 e depois vamos fazendo sempre o dobro do anterior (16, 32, 64, 128, 256…):

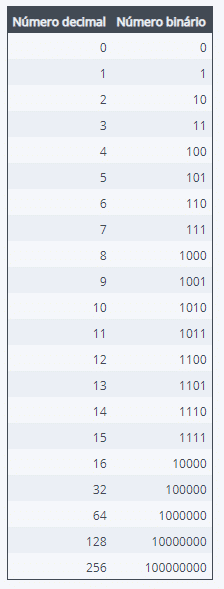
Para fazer a conversão utilizando essa tabela, você pega o valor binário do decimal mais próximo do número a ser convertido, e faz uma subtração. Por exemplo: 347 – 256 = 91, agora você vai pegar na tabela o número mais próximo de 91, que nesse caso é 64. Fazendo a subtração temos 27. Mesma coisa, qual o número próximo a 27 na tabela? 16 e aí por diante…  O número 347 pode expressar-se como: 256 + 64 + 16 + 8 + 2 + 1. Com isso, 347 corresponde a 101011011 em binário.

Observe que nessa tabela paramos no 256, mas você pode ir dobrando de valor para gerar em números maiores, por exemplo, o número 2347 pode expressar-se como: 2048 + 256 + 32 + 8 + 2 + 1 e o seu resultado seria  100100101011 em binário.

Agora vou demonstrar porque o binário trabalha dobrando os seus valores. Lembra que o binário é base 2? Então temos: 

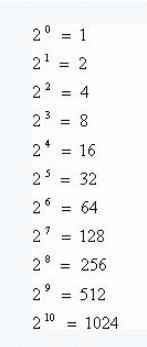
Sistema de numeração Hexadecimal

Como você pode perceber, no sistema binário são necessários muitos dígitos para representar números relativamente pequenos, o que dificulta o trabalho das pessoas que programam os computadores. Para solucionar este problema usa-se frequentemente o sistema de numeração hexadecimal. Vem do hexa=6 e deci=10, sistema numérico de base 16. Ele vai de 0 à 10 e utiliza A,B,C,D,E e F que representam 10,11,12,13,14 e 15 respectivamente. Então fica assim: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E e F.

Pense o seguinte, lembra que expliquei sobre o agrupamento de binário, onde 8 bits agrupados correspondem a 1 byte? Se você observar, 1 byte pode ser representado por 8 algarismos do sistema binário ou por 2 algarismos do sistema hexadecimal. Veja um exemplo de como fica mais simples a representação com o sistema Hexadecimal:

Com é feito a conversão de Decimal para  Hexadecimal?

Assim como no Binário, para esta conversão, dividiremos o número decimal por 16 sucessivas vezes, separando sempre o seu resto e continuando a dividir o seu quociente até que ele seja menor que 16. Por fim, a sequência inversa dos restos, de baixo para cima, você terá sua conversão. Veja os exemplos:

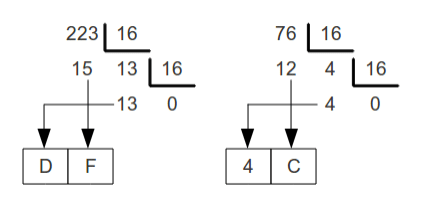
223 em decimal é equivalente a DF em hexadecimal, da mesma forma 76 = 4C em hexadecimal.

Com esses sistemas são possíveis você fazer as conversões opostas também. Converter de binário para decimal, binário para hexadecimal, octal, etc… Idem para hexadecimal, decimal e octal que podem gerar conversões entre si.

Mais detalhes sobre o Sistema Hexadecimal, você encontra no artigo Sistema de Numeração Hexadecimal

Sistema de numeração Octal

Antigamente o Sistema octal era a principal  alternativa mais compacta ao binário na programação em linguagem de máquina. Atualmente, o sistema hexadecimal é mais utilizado como alternativa ao binário. Esse sistema tem base 8 e compreendem os números 0, 1, 2, 3, 4, 5, 6 e 7. Como os anteriores, para converter um número decimal para octal, basta realizar divisões sucessivas do número decimal por 8. Veja:

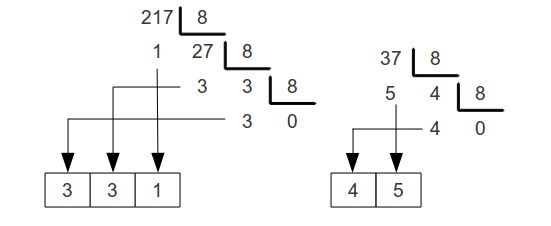
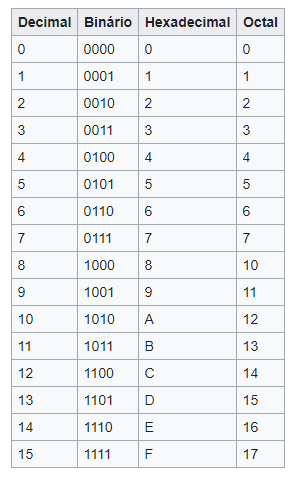
No artigo anterior, falei sobre a tabela ASCII, volte lá e veja se agora aquela tabela vai fazer mais sentido para você. Com certeza, agora você conseguirá ler a tabela ASCII e interpretar a sua utilização de forma mais contundente. Na tabela a seguir você terá uma visão geral de todos os sistemas explicados aqui e mostrando a relação dos seus valores entre si:

Caso ainda tenha alguma dificuldade e precise gerar os cálculos mais rapidamente, utilize nossa calculadora: https://growthcode.com.br/calculadora-de-conversao-de-bases-numericas/

É isso aí! Esses termos são muito importantes para a sua base como programador ou programadora. Para construir uma carreira sólida, obviamente você vai precisar de uma base sólida em sua formação.

Se você já chegou a um patamar mais elevado no mundo da programação, já está na hora de você se aprofundar em conceitos mais importantes como qualidade de código e padrões de projetos.

Escrevi o livro “Além do Código” para desenvolvedores que querem ser mais do que meros codificadores. É um guia completo que aborda todos esses tópicos avançados de forma prática e didática.

Se você está realmente comprometido em não ficar para trás, não perca tempo e adquira agora.

Confiança Sempre!!!

Fontes:

• https://www.inf.ufsc.br/~bosco.sobral/extensao/sistemas-de-numeracao.pdf
• https://pt.calcuworld.com/calculadoras-matematicas/calculadora-binaria/
• https://calculareconverter.com.br/converter-decimal-para-octal/
• https://dicasdeprogramacao.com.br/as-10-conversoes-numericas-mais-utilizadas-na-computacao/
• https://pt.wikibooks.org/wiki/Eletr%C3%B4nica_Digital/Sistemas_de_Numera%C3%A7%C3%A3o
• https://pt.wikibooks.org/wiki/Eletr%C3%B4nica_Digital/Sistemas_de_Numera%C3%A7%C3%A3o