Métricas Avançadas : Explorando a Média Winsorizada, Média de Médias, Desvio Absoluto Mediano e Média Logarítmica

Atualizado pela última vez em 1 de dezembro de 2023

As métricas mencionadas são empregadas em cenários distintos de análise de dados para fornecer insights mais aprofundados e mitigar a influência de outliers, o que é crucial para a interpretação precisa dos dados. Abaixo, apresento uma exploração de cada uma dessas métricas:

Média Winsorizada

A Média Winsorizada é uma medida estatística robusta que surgiu como uma alternativa à média aritmética tradicional para mitigar a influência de valores aberrantes, conhecidos como outliers, em um conjunto de dados. Esta métrica foi introduzida por Charles P. Winsor, um engenheiro que se tornou biostatístico, na primeira metade do século 20, com o objetivo de proporcionar estimativas estatísticas mais confiáveis na presença de outliers​

Os outliers são valores extremos que podem distorcer significativamente a média aritmética de um conjunto de dados, levando a interpretações incorretas e a modelos de aprendizado de máquina imprecisos. 

A fórmula para calcular a média Winsorizada é relativamente simples. Primeiro, os dados são ordenados. Em seguida, um percentual especificado de valores nas extremidades baixa e alta da distribuição é substituído pelos valores mais extremos restantes. Finalmente, a média dos valores substituídos é calculada, conforme a seguinte fórmula:

Onde:

• x̅_w​ é a média Winsorizada.
• n é o número total de observações no conjunto de dados.
• X_i​ são os valores do conjunto de dados após a substituição dos outliers.

Para você contextualizar melhor, suponha que temos o seguinte conjunto de dados já ordenado: {2, 4, 7, 7, 30, 50}. O percentual de Winsorização (20% neste caso) determina a proporção de valores nas extremidades da distribuição que serão substituídos. Como o conjunto de dados tem 6 valores, 20% de 6 é 1,2. Como não podemos ter uma contagem fracionária de valores, normalmente arredondamos para o número inteiro mais próximo, que neste caso seria 1.

Substitua o menor e o maior valor no conjunto de dados pelos próximos valores mais extremos. Neste caso, substituímos o valor 2 pelo próximo valor mais alto, que é 4, e substituímos o valor 50 pelo próximo valor mais baixo, que é 30. Isso resulta no conjunto de dados Winsorizado: {4, 4, 7, 7, 30, 30}

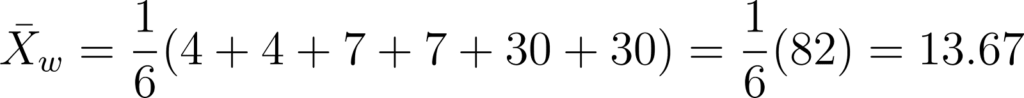
Portanto, a Média Winsorizada para este conjunto de dados, com 20% de Winsorização, é 13.67.

Tanto a Média Winsorizada quanto a Média Truncada são úteis para mitigar a influência de outliers, mas enquanto a Média Truncada descarta os valores extremos, a Média Winsorizada os substitui, mantendo o tamanho da amostra.

Média de Médias

A Média de Médias é uma abordagem estatística utilizada quando se deseja agregar informações de diferentes amostras, calculando a média aritmética de várias médias aritméticas provenientes dessas amostras. Esta estratégia pode ser útil em cenários onde há a necessidade de consolidar informações de diferentes fontes ou grupos de dados.

Em cenários de análise de dados, é comum encontrar situações onde várias amostras de dados são coletadas e analisadas separadamente. Cada uma dessas amostras pode ter sua própria média aritmética, que resume a tendência central dos dados naquela amostra. A Média de Médias é uma técnica que busca consolidar essas informações, proporcionando uma visão agregada da tendência central entre todas as amostras.

Para você entender melhor, imagine que temos três conjuntos de dados, cada um representando as vendas diárias de três lojas diferentes ao longo de um mês. Os conjuntos de dados são:

• Loja A: {100,150,200,250,300}
• Loja B: {50,75,100,125}
• Loja C: {200,250,300,350,400,450,500}

As médias aritméticas para cada loja são:

• Para a Loja A: 

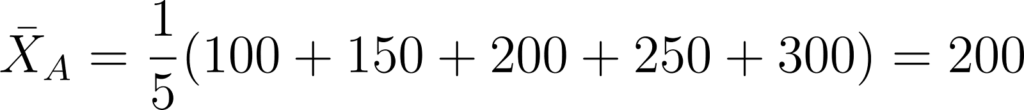
• Para a Loja B: 

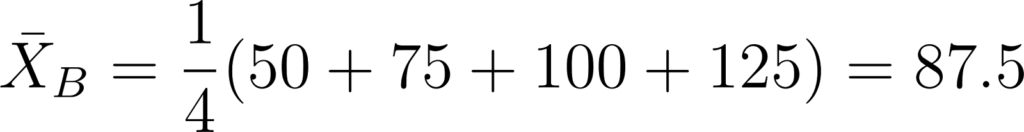
•   Para a Loja C: 

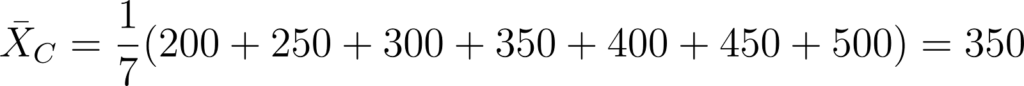
Para calcular a Média de Médias, você deve somar as médias aritméticas individuais de cada conjunto de dados (neste caso, cada loja) e dividir pelo número total de conjuntos de dados. A fórmula é dada por:

onde:

• m é o número total de conjuntos de dados,
• X̅_i​ são as médias aritméticas individuais de cada conjunto de dados.

Substituindo os valores das médias aritméticas das lojas A, B e C na fórmula, obtemos:

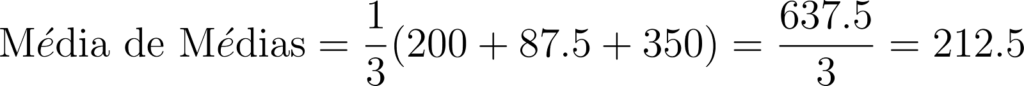
Portanto, a Média de Médias das vendas diárias entre as três lojas é de 212.5 unidades vendidas por dia.

É importante notar que a Média de Médias pode, às vezes, levar a interpretações enganosas, especialmente se as amostras tiverem tamanhos muito diferentes ou variâncias distintas. Por exemplo, uma média de médias pode ser distorcida por uma média aritmética extremamente alta ou baixa de uma amostra muito pequena.

Desvio Absoluto Mediano

A Desvio Absoluto Mediano (MAD, do inglês Median Absolute Deviation) é uma medida de dispersão estatística utilizada para quantificar a variabilidade em um conjunto de dados univariados, calculando-se a mediana das diferenças absolutas entre cada valor do conjunto de dados e a mediana geral desse conjunto:

Onde:

• x_i​ são os valores individuais no conjunto de dados,
• x_m​ é a mediana do conjunto de dados​​.

Para você fixar o entendimento, suponha que temos o seguinte conjunto de dados:

X = {10, 20, 30, 40, 50}

Como os dados já estão ordenados e a quantidade de elementos da nossa amostra é ímpar, a mediana é 30.

Agora podemos calcular as diferenças absolutas entre cada valor de X e a mediana: Quando você ver a palavra “diferença”, já imagine uma subtração. As coisas absolutas, que forem representadas entre dois sinal “|”, significa que o valor vai ser sempre positivo. Ou seja, a diferença​a Absoluta = ∣a−b∣ 

Voltando para o nosso conjunto de dados, teremos as diferenças absolutas entre cada valor de XX e a mediana desta forma::

• ∣10−30∣ = 20
• ∣20−30∣ = 10
• ∣30−30 ∣= 0
• ∣40−30 ∣= 10
• ∣50−30 ∣= 20

Ao ordenarmos este dados para tirar a mediana deste novo conjunto, teremos  {0,10,10,20,20}, logo, como a quantidade de elementos do conjunto é ímpar, temos as Mediana das diferenças absolutas = 10.

Média Logarítmica

A Média Logarítmica é uma medida estatística utilizada em conjuntos de dados onde os valores têm uma relação multiplicativa ou exponencial entre si. É especialmente útil em contextos onde o uso de médias aritméticas tradicionais poderia ser enganoso devido à natureza dos dados. Isso é comum em campos como a economia (para taxas de crescimento), biologia (por exemplo, na análise de taxas de crescimento populacional), ou em qualquer área onde os dados possam variar por ordens de magnitude.

A fórmula para a média logarítmica de dois números positivos x e y é definida como:

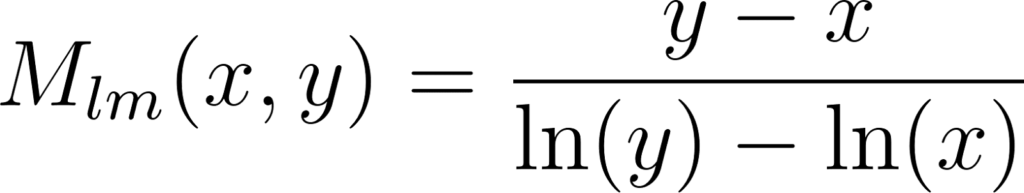
Onde:

• x e y são os números positivos para os quais estamos calculando a média logarítmica. É importante notar que tanto x quanto y devem ser maiores que zero, pois o logaritmo de zero ou de números negativos não é definido no conjunto dos números reais.
• ln⁡(y) e ln⁡(x) são os logaritmos naturais de y e x, respectivamente. O logaritmo natural é o logaritmo com base e, onde e é a constante de Euler, aproximadamente igual a 2.71828.
• A expressão ln⁡(y)−ln⁡(x) é a diferença entre os logaritmos de y e x, e fornece uma medida da variação relativa entre x e y.

Se x=y, então a diferença entre os logaritmos no denominador seria zero, o que causaria uma divisão por zero. Nesse caso, a fórmula não se aplica e a média logarítmica é simplesmente x (ou y), já que não há variação entre os dois números.

Vamos criar um exemplo passo a passo para calcular a média logarítmica de dois números, digamos 4 e 16, que são convenientes porque são potências de 2 e nos dão logaritmos naturais “limpos”.

Substituindo x e y com os valores dados, temos: 

• ln⁡(4) é aproximadamente 1.386
• ln⁡(16) é aproximadamente 2.773
• A diferença é 2.773 − 1.386 = 1.387

Assim, a média logarítmica de 4 e 16 é aproximadamente 8.651.

A média logarítmica é amplamente utilizada em engenharia e ciências físicas. Um exemplo clássico é o cálculo da diferença de temperatura média logarítmica em trocadores de calor. Esse cálculo é fundamental para determinar a eficiência de transferência de calor entre dois fluidos que estão em temperaturas diferentes.

Em conclusão, este artigo oferece uma visão abrangente de métricas estatísticas robustas, destacando a importância de se adaptar às peculiaridades dos conjuntos de dados para extrair interpretações precisas e significativas. 

A escolha apropriada dessas métricas depende do entendimento claro dos dados em análise e dos objetivos da investigação. A prudência na escolha e interpretação de métricas estatísticas robustas como essas pode conduzir a insights mais confiáveis e a decisões baseadas em dados mais fundamentadas. Assim, essas métricas não são apenas ferramentas matemáticas, mas são também aliadas estratégicas na navegação pelo crescente mar de dados em que nos encontramos na era da informação.

Se você gostou deste artigo, demonstre deixando o seu comentário e compartilhando com outras pessoas que podem se beneficiar deste conteúdo. Nos vemos no próximo artigo!

Confiança Sempre!!! 

Referências:

1. WIKIPEDIA. Winsorized mean. Disponível em: https://en.wikipedia.org/wiki/Winsorized_mean. Acesso em: 05 nov. 2023​.
2. SPRINGERLINK. An Analysis of Winsorized Weighted Means. Disponível em: https://link.springer.com/article/10.1007/s00362-011-0376-3. Acesso em: 05 nov. 2023​.
3. SCIENCE DIRECT. Winsorization – an overview. Disponível em: https://www.sciencedirect.com/topics/mathematics/winsorization. Acesso em: 05 nov. 2023​.
4. CROSS VALIDATED. Will the mean of a set of means always be the … Disponível em: https://stats.stackexchange.com/questions/31177/will-the-mean-of-a-set-of-means-always-be-the-mean-of-the-entire-set. Acesso em: 05 nov. 2023​.
5. NIST. The biweight transformation. Disponível em: https://www.itl.nist.gov/div898/software/dataplot/refman2/ch2/biweight.pdf. Acesso em: 05 nov. 2023​.
6. NIST. Biweight Midvariance. Disponível em: https://www.itl.nist.gov/div898/software/dataplot/refman2/ch2/biwmidv.pdf. Acesso em: 05 nov. 2023​.
7. NIST. Biweight Scale. Disponível em: https://www.itl.nist.gov/div898/software/dataplot/refman2/ch2/biwscale.pdf. Acesso em: 05 nov. 2023​.
8. SPRINGERLINK. Tukey’s biweight estimation for uncertain regression model with … Disponível em: https://link.springer.com/article/10.1007/s11075-020-00908-3. Acesso em: 05 nov. 2023​.
9. CROSS VALIDATED. Why (or when) to use the log-mean? Disponível em: https://stats.stackexchange.com/questions/790/why-or-when-to-use-the-log-mean. Acesso em: 05 nov. 2023​
10. CRAN. Biweight Midvariance. Disponível em: https://cran.r-project.org/web/packages/biwt/biwt.pdf. Acesso em: 05 nov. 2023.
11. WIKIPEDIA. Biweight midcorrelation. Disponível em: https://en.wikipedia.org/wiki/Biweight_midcorrelation. Acesso em: 05 nov. 2023.
12. PUBMED. A robust alternative to the S-Plus biweight estimates. Disponível em: https://pubmed.ncbi.nlm.nih.gov/10737580/. Acesso em: 05 nov. 2023.
13. NIST. 1.3.6.7.1. Tukey’s Biweight Function. Disponível em: https://www.itl.nist.gov/div898/software/dataplot/refman2/ch2/weightsa.htm. Acesso em: 05 nov. 2023.
14. NIST. Biweight Midvariance. Disponível em: https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/biwemiva.htm. Acesso em: 05 nov. 2023​.
15. MOSTELLER, F.; TUKEY, J.W. Data Analysis and Regression: A Second Course in Statistics. Addison-Wesley, 1977, pp. 203-209.
16. ASTROPY. biweight_midvariance — Astropy v5.3.3. Disponível em: https://docs.astropy.org/en/stable/api/astropy.stats.biweight_midvariance.html. Acesso em: 05 nov. 2023​.
17. NIST. Biweight Midvariance. Disponível em: https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/biwemiva.htm. Acesso em: 05 nov. 2023​.
18. WIKIPEDIA. Robust measures of scale. Disponível em: https://en.wikipedia.org/wiki/Robust_measures_of_scale#The_biweight_midvariance. Acesso em: 05 nov. 2023​.
19. JAMESON, G.; MERCER, P. R. The Logarithmic Mean Revisited. Taylor & Francis Online.
20. On bounds of logarithmic mean and mean inequality chain. arXiv.org.
21. Extension of Power Mean and Logarithms Mean. Science Publishing Group.
22. CARLSON, B. C. The Logarithmic Mean. The American Mathematical Monthly.
23. Best practices in statistics. SAGE Journals.