O que um programador precisa saber sobre matemática?

Muitos quando veem a palavra matemática, já dá dor de barriga, medo, calafrio e vontade de sumir kkkkk Mal sabem eles a beleza que existe na matemática! Eu sou suspeito, porque gosto bastante. E aí? Porque você acha que programador precisa saber muito sobre matemática? Já vou dando um spoiler… Para ser programador você não precisa ser um prodígio da matemática, mas você precisa de um mínimo de conhecimento para conseguir assimilar os conceitos que envolvem a programação.

Resumidamente e sem exageros, você precisa saber como pré-requisito para iniciar em programação, as 4 operações básicas: soma, subtração, multiplicação e divisão. Só isso já te permite dar os primeiros passos no estudo rumo a ser tornar um programador ou uma programadora.

Essas operações básicas, você precisa conhecer as suas precedências. Ou seja, saber a ordem em que elas deve ser escrita e qual operador tem mais poder sobre o outro, o resto, o próprio mecanismo das linguagens de programação se encarregará de fazer a execução e cálculo.  Expliquei sobre as precedências dos operador no artigo Principais características de uma linguagem de programação e sua escrita – parte 4, vai lá e dá uma revisada.

Outra questão que assusta bastante são operações que enxergamos como complexas, como exemplo a expressão 456879 dividido por 4567. Se você fosse fazer manualmente esse cálculo, via papel e caneta, seria realmente uma tarefa difícil, já em programação você vai fazer apenas a expressão 456879 / 4567 (Isso eu também explico no artigo indicado a acima)

Até aí tudo bem!!! Você já começou a perder o medo do uso da matemática através das facilidades que as linguagens de programação trás. Mas, se você ficar só nesses conhecimentos básicos, você vai ser tornar um programador “mediano” frente à outras possibilidades, por exemplo de otimizar os seu códigos e deixar ele mais performático. Não só isso, mas ter uma boa base matemática, vai te livrar por exemplo de utilizar algumas métricas, como a média de forma errada. Quer ver um exemplo? Vamos lá!!!

Interpretando a média matemática corretamente

Imagine que você tem um logger gerando logs em um método de uma classe para medir o seu desempenho. Digamos que você executou o método 6 vezes, com os seguintes tempos:

• 1ª execução levou 1s (um segundo)
• 2ª execução levou 1.1s
• 3ª execução levou 0.9s
• 4ª execução levou 1.5s
• 5ª execução levou 0.5s
• 6ª execução levou 10s

Se eu te perguntar, qual foi o tempo médio de execução do método? Se você não lembra como fazer o cálculo de média, é só somar todos os valores e dividir pela quantidade de elementos. Nesse exemplo é (1 + 1.1 + 0.9 + 1.5 + 0.5 + 10) / 6  = 2.5 de média. Agora me responde: Está certo utilizar a média para medir o ponto médio de dessa amostra dos tempos? Observe que 5 das 6 execuções o tempo ficou entre 1 e 1.5 segundos. Percebe o problema que há em não saber utilizar as métricas corretamente? Nesse exemplo, a média foi 2.5, porém na totalidade não passou de 1.5, ou seja, utilizar a média para esse exemplo iria distorcer a sua análise. Veja a seguir algumas alternativas.

Quando a média não basta, podemos procurar a mediana

A mediana é outra métrica importante em que podemos utilizar para detectar se o uso da média está correta em nossa análise. Seu uso é bastante simples, você pega todos os valores da sua amostra e faz uma ordenação do menor para o maior valor (0.5, 0.9, 1, 1.1, 1.5, 10), e pega o valor do meio dessa lista. Contudo, tem um detalhe… Se o total de elementos da lista for ímpar, o valor do meio já fica visível (exemplo, 1, 1, 2, 3, 3 a mediana é 2), como essa lista do nosso exemplo a quantidade é par (6), temos que pegar os 2 valores do centro (0.5, 0.9, 1, 1.1, 1.5, 10) somar e dividir por 2, nesse caso (1 + 1.1) / 2 = 1.05. Agora sim!!! Está bem mais próximo da nossa realidade, não é verdade? Só o fato de você conhecer média e mediana, já vai ser um diferencial para você enquanto programador ou programadora!!! 

Vamos dificultar um pouco mais a análise. Imagine agora que você fez a execução do seu método 10 vezes e o comportamento foi o seguinte:

• 1ª execução levou 1s (um segundo)
• 2ª execução levou 1s
• 3ª execução levou 1s
• 4ª execução levou 1s
• 5ª execução levou 1s
• 6ª execução levou 4s
• 7ª execução levou 4s
• 8ª execução levou 6s
• 9ª execução levou 6s
• 10ª execução levou 7s

Se formos calcular a média, chegaremos a (1 + 1 + 1 + 1 + 1 + 4 + 4 + 6 + 6 + 7)/10 = 3.2, será que podemos utilizar a média para essa amostra kkkk? Continuei lendo…  Será que a mediana agora vai ser uma boa escolha? Vamos calcular! Lembrando, primeiro devemos listar os valores do menor para o maior (1, 1, 1, 1, 1, 4, 4, 6, 6, 7) e como a quantidade é par (10), vamos pegar o valor central e dividir por dois (1 + 4) / 2 = 2.5. Puts! agora complicou kkkk!!! O valor mediano definitivamente não é uma boa escolha porque 50% da nossa amostra têm valore médio de 1 e os demais 50%  tem média de 5.4. E agora kkk?

Se tem muito números repetidos, eles estão na moda

Podemos tentar resolver o problema da análise anterior utilizando outro recurso chamado moda, que também é uma métrica de medidas de tendência central assim como a média e a mediana. Qual a ideia da moda? Simplesmente encontrar os valores que mais se repetem dentro de uma amostra. Para achar a moda, ordene os números assim como na mediana e observe quais são os números que mais se repetem (1, 1, 1, 1, 1, 4, 4, 6, 6, 7) nesse caso, a moda é 1. Agora que temos três possíveis números para utilizamos como resultado, média = 3.2, mediana = 2.5 e moda = 1, qual deles utilizar?

E quando a média, mediana e moda não são suficientes para uma análise de tendência central?

Temos mais recursos para tentarmos encontrar o número ideal para análise. No exemplo anterior utilizamos uma média chamada média aritmética. Mas, podemos utilizar também a média chamada média ponderada ou média aritmética ponderada – Calma!! Não sai correndo ainda kkkk –  Para achar a média ponderada, você vai contar a quantidade de repetições de cada valor e criar um “peso” para cada número. Vamos pegar esses pesos, e vamos multiplicar pelos valores. Por exemplo, o 1 se repete quantas vezes? 5 vezes. Já o 4 e 6 só se repetem 2 vezes, e o 8 uma vez. Fica assim: (1 * 5) + (1 * 5) + (1 * 5) + (1 * 5) + (1 * 5) + (4 * 2) + (4 * 2) + (6 * 2) + (6 * 2) + (7 * 1) = 72. Agora vamos somar os pesos (5 + 5 + 5 + 5 +  5 + 2 + 2 +  2 + 2 + 1)  = 34. Como isso pegamos o produto da soma dos valores pelos pesos e dividimos pela soma dos pesos (72 / 34) = 2.11. Pronto! A média ponderada é 2.11.

Você deve estar pensando: Walmir? Agora você bugou minha mente kkkk! Percebe que não é uma tarefa fácil, apenas utilizando recursos simples e básicos da matemática? Então meu amigo e minha amiga, não fiquem apenas no básico! Estude um pouco mais de matemática para não cair em problemas de análise como esse.

Estou generalizado e chamando tudo de matemática porque a estatística é um ramo da matemática que trata da coleta, da análise, da interpretação e da apresentação de massas de dados numéricos.

A média ponderada é usada principalmente para evitar distorções no valor médio, ao considerar os pesos individuais de cada valor

E agora, qual métrica utilizar kkkkk? Calma! No estudo da estatística, conseguimos medir o quão dispersos os números de nossa amostra estão distantes um do outro. Para isso temos a variância e o desvio padrão.

Como calcular a variância?

Continuando com a mesma lista de valores do último exemplo, para calcularmos a distância entre os números, pegamos cada valor e subtraímos pelo valor da média geral e elevamos ao quadrado. Sabemos que a média é 3.2, então fazemos assim: 

((1 – 3.2)^2) = 4.84

((1 – 3.2)^2) = 4.84 

((1 – 3.2)^2) = 4.84

((1 – 3.2)^2) = 4.84 

((1 – 3.2)^2) = 4.84

((4 – 3.2)^2) = 0.64 

((4 – 3.2)^2) = 0.64

((6 – 3.2)^2) = 7.84

((6 – 3.2)^2) = 7.84

((7 – 3.2)^2) = 14.44

Agora somamos esses valores e dividimos pelo total da nossa amostra menos 1 (10 – 1), assim:

(4.84 + 4.84 + 4.84 + 4.84 + 4.84 + 0.64  + 0.64 + 7.84 + 7.84 + 14.44) / (10 – 1) = 6.17

Para esse exemplo a variância é de 6.17, agora conseguimos calcular o desvio padrão. O desvio padrão é uma medida que indica a dispersão dos dados dentro de uma amostra com relação à média. Ou seja, a dispersão é o quanto os números de um mesmo intervalo estão longe do centro (média). Para achar o desvio padrão, basta fazer a raiz quadrada da variância, nesse caso o desvio padrão é 2.48.

Para você fixar o conhecimento sobre desvio padrão, se você pegasse uma amostra mais homogênea como 3, 5, 3.5, 4, 6, 4.2, 3.9, 3.8, 4.1 você teria a média = 4.16, variância = 0.76 e desvio padrão = 0.87. O que isso significa? Quanto menor o desvio padrão, mais os números estão próximos da média. Sacou?

Enfim… Essa é uma base super interessante para você conhecer sobre estatística para conseguir fazer medições com mais assertividade.  Além disso, em muitos casos, você vai se deparar com outro tipo de representação matemática, utilizando símbolos e fórmulas como: 

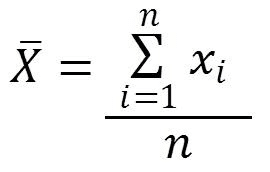
Se você chegou até aqui, você já sabe com calcular a média, correto? Então não saia correndo fugindo dessa fórmula kkkkk  Essa fórmula nada mais que é a fórmula da média. o X com um traço em cima, corresponde a uma variável que vai armazenar o resultado final da média. O símbolo maior e estranho chama-se somatório. O n corresponde a quantidade de elementos da sua lista, no nosso primeiro exemplo de média seria n=6 e no último n=10.  Esse i é o que representa o índice dos elementos a serem somados (i=1, i=2, i=3, i=4 … in=10).  Se você já viu a representação o i em programação dentro do laço FOR, vai notar que é a mesma ideia for (i=1; i <= N; i++). O xi está representando cada valor segundo o seu índice, no nosso primeiro exemplo, podemos representar os índices assim  X1 = 0.5, X2 = 0.9, X3 = 1, X4 = 1.1, X5 =1.5 e  X6 =10. É basicamente isso! Veja outra forma de representação da formula da média:

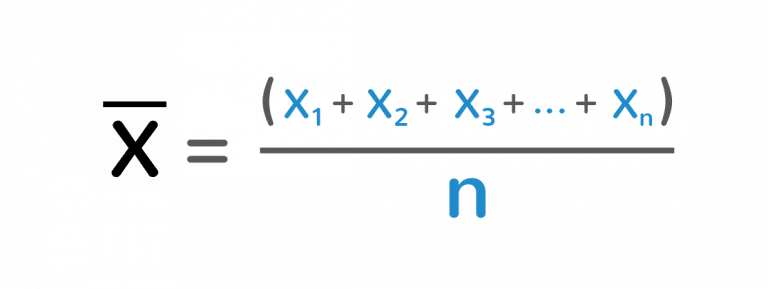
Às vezes, você vai encontrar fórmulas ou pouco mais complexas para o mesmo tipo de resultado. Mas, agora que você já consegue interpretar o somatório, fica mais fácil entender outras fórmulas, como a fórmula a seguir que é bem mais elaborada:

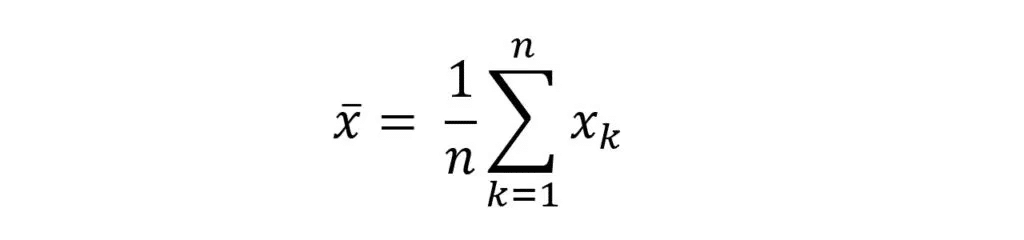
Não fique trista, mas, essa também é a fórmula da média, só que expressa de forma diferente kkkk. A interpretação dessa forma é 1 sobre n multiplicado pelo somatório dos elementos.  A primeira fórmula anterior, você interpreta como o somatório dos elementos divididos por n elementos. Observe que nessa figura logo acima, trocamos o i por k. Mas poderia ser qualquer letra, z, a, o, m, etc… O resultado acaba sendo o mesmo. Sacou?

Para você poder analisar e praticar, segue a fórmula que define o desvio padrão, onde você lê com raiz quadrada do somatório dos elementos x menos a média geral elevado essa soma ao quadrado, dividindo pelo número n:

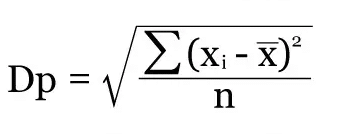
Como você bem sabe, a matemática é um mundo bastante vasto. O que vai determinar o seu nível de necessidade de conhecimentos em matemática, vai ser o tipo de problema que você precisa resolver utilizando a matemática. Se você for construir, por exemplo, soluções para Machine Learning ou Data Science, você precisará de uma base um pouco melhor. Mas, para construção de soluções mais comerciais, em sua grande maioria, não vai fazer uso de tantos recursos matemáticos assim. Enfim… Para começar, o que expliquei aqui já vai ser de grande ajuda para você entender os próximos conceitos que vou mostrar, quando entrarmos no mundo dos algoritmos e medições de complexidade dos seus códigos. Leia e releia este artigo quantas vezes for necessário até aprender definitivamente, ok? Até o próximo artigo!

Confiança Sempre!!!

Fontes:

• https://pt.khanacademy.org/math
• https://www.todamateria.com.br/matematica/estatistica/