Atualizado pela última vez em 30 de outubro de 2023
A estatística, como uma disciplina distinta, começou a tomar forma no século XVII, embora as raízes de coleta e interpretação de dados remontam à antiguidade. A evolução dos símbolos estatísticos é um reflexo da contínua busca da humanidade por compreender e interpretar o mundo ao nosso redor de maneira precisa e eficaz, como foi explanado no artigo anterior sobre “A Evolução da Notação Matemática”. Os símbolos na estatística também desempenham um papel vital, pois oferecem uma linguagem comum para a expressão de ideias complexas, facilitando a comunicação entre os profissionais.
O Surgimento da Estatística
A estatística tem suas raízes em contagens de censos realizados milhares de anos atrás, mas como uma disciplina científica distinta, foi desenvolvida no início do século XIX, se concentrando inicialmente no estudo de populações, economias e ações morais. Posteriormente, no mesmo século, evoluiu como uma ferramenta matemática para a análise desses números. No entanto, o marco inicial da estatística é frequentemente datado de 1662, quando John Graunt, junto com William Petty, desenvolveu métodos estatísticos e de censo humanos iniciais que forneceram uma estrutura para a demografia moderna, com Graunt produzindo a primeira tabela de vida, fornecendo probabilidades de sobrevivência para cada idade.
O termo “estatística” foi introduzido pela primeira vez pelo acadêmico alemão Gottfried Achenwall no meio do século XVIII. Achenwall usou a palavra para se referir à ciência do estado (statecraft) em relação à coleta e uso de dados pelo estado. Este uso inicial refletia a importância da coleta de dados para as operações e administração do estado, especialmente em áreas como a contagem da população e a coleta de informações econômicas. A estatística, nesse contexto, estava intimamente ligada ao governo e à administração pública. Foi um passo inicial importante na formalização da estatística como um campo de estudo, focado em coletar, analisar e interpretar dados para tomar decisões informadas.
A estatística evoluiu como uma disciplina científica distinta no início do século XIX, expandindo seu escopo para incluir o estudo de populações, economias e ações morais. Posteriormente, durante esse século, a estatística começou a ser vista como uma ferramenta matemática para analisar números relacionados a esses e outros temas, pavimentando o caminho para o desenvolvimento de métodos estatísticos avançados que são amplamente utilizados hoje.
Símbolos Estatísticos: A Compreensão dos Dados
A criação de símbolos estatísticos tem acompanhado o desenvolvimento da estatística como uma disciplina científica e a lista de símbolos é bastante extensa. Vamos explorar a jornada de alguns símbolos estatísticos cruciais, no que tangem aspectos importantes para Data Science, Machine Learning e suas origens:
Média Aritmética (x̅ ou μ):
A notação para a média aritmética tem suas raízes em conceitos matemáticos antigos, mas a notação moderna usando x̅ (para uma amostra) e μ (para uma população) se tornou comum a partir do século XIX, com o advento da teoria da probabilidade e da estatística moderna. O μ (pronuncia-se “mi”), quando você vê o μ você sabe que é um parâmetro e que esse símbolo representa a média.
A população refere-se ao conjunto completo de indivíduos, itens ou dados que estão sendo estudados.Exemplo: Se quisermos estudar a altura de todos os estudantes de uma universidade, a população seria a altura de TODOS os estudantes dessa universidade. Uma amostra é um subconjunto da população que é selecionada para análise. Exemplo: Em vez de medir a altura de todos os estudantes da universidade (o que poderia ser muito demorado e caro), podemos selecionar um grupo de 100 estudantes aleatoriamente e medir suas alturas. Esses 100 estudantes formariam uma amostra da população da universidade.
A média, como você já sabe, é obtida somando todos os valores no conjunto de dados e dividindo pelo número total de valores. Porém, existem diversos tipos de médias, cada uma com suas próprias características e aplicabilidades dependendo do contexto dos dados em questão. Posteriormente vamos abordar outros elementos simbólicos que tangem o tema sobre médias bem como a exploração geral das principais representações em fórmulas completas fazendo um comparativo entre a sua representação e a aplicabilidade prática utilizando uma linguagem de programação qualquer..
Variância (s² ou σ²):
A variância, como uma medida de dispersão, foi introduzida por Ronald A. Fisher, um estatístico e biólogo britânico, em 1918. Fisher introduziu o conceito de variância para avaliar a dispersão de conjuntos de dados. A notação moderna usando s² (para uma amostra) e σ² (“sigma” ao quadrado, para uma população) se solidificou ao longo do tempo, refletindo a estrutura simbólica da matemática.
Uma medida de dispersão indica quão espalhados ou agrupados estão os valores em um conjunto de dados. É como uma ferramenta que nos ajuda a entender o quão longe os valores estão do centro ou da média do conjunto de dados. Para você contextualizar melhor, imagine que você está jogando dardos. Se todos os seus dardos acertarem bem próximo ao centro do alvo, eles têm uma baixa dispersão. Por outro lado, se os dardos acertarem pontos muito diferentes no alvo, longe um do outro, eles têm uma alta dispersão.
O termo “variância” foi proposto para indicar a variação ou a dispersão dos valores em um conjunto de dados em relação à média desses valores. É uma maneira de expressar o quão distante os valores estão, em média, do valor central (média). A variância é especialmente útil em situações onde é importante conhecer a estabilidade ou consistência dos dados.
Calcular a variância é um processo de alguns passos simples:
- Primeiro, encontre a média (a média aritmética) dos seus dados somando todos os valores e dividindo pelo número total de valores.
- Em seguida, subtraia a média de cada valor nos seus dados. Isso lhe dará uma ideia de quão longe cada valor está da média.
- Agora, eleve cada uma dessas diferenças ao quadrado. Isso é feito para garantir que todas as diferenças sejam positivas (pois qualquer número elevado ao quadrado é positivo). Isso é importante porque as diferenças negativas poderiam cancelar as diferenças positivas, dando uma falsa impressão de que não há variância.
- Por último, encontre a média desses quadrados. Some todos os quadrados que você obteve no passo anterior e divida pelo número total de valores (para a variância da população) ou pelo número de valores menos um (para a variância da amostra).
Elevando as diferenças ao quadrado, eliminamos a possibilidade de valores negativos que poderiam distorcer a verdadeira dispersão dos dados. Além disso, ao elevar ao quadrado, damos mais peso às diferenças maiores, o que pode ser informativo quando queremos entender a dispersão em nossos dados.
A métrica a seguir, Desvio Padrão, utiliza todo o trabalho da variância para restaurar as proporcionalidades mais próximas dos valores originais. Para não ficar tão abstrato, imagine que você está medindo a altura de seus amigos em metros. A média (altura média) é fácil de entender porque está na mesma unidade: metros.
Agora, quando calculamos a variância, nós elevamos as diferenças ao quadrado, então a unidade muda para metros quadrados. Isso pode ser difícil de entender porque não estamos mais na mesma “linguagem” dos dados originais, que é metros.
Aqui é onde o desvio padrão entra: ao tirar a raiz quadrada da variância, voltamos para a unidade original, que é metros, tornando a informação mais fácil de entender e comparar com a média.
Desvio Padrão (s ou σ):
O desvio padrão é uma métrica estatística que também foi popularizada por Ronald A. Fisher. Como já expliquei anteriormente, para fortalecer um pouco mais o seu entendimento, vamos desdobrar os conceitos de variância e desvio padrão através de um exemplo simples.
Suponha que temos dois conjuntos de dados que representam as notas de dois diferentes grupos de estudantes em um teste:
- Grupo 1: {90,92,91,89,93,91}
- Grupo 2: {70,85,55,80,95,60}
Vamos calcular a variância para o Grupo 1 e Grupo 2:
- Média do Grupo 1:
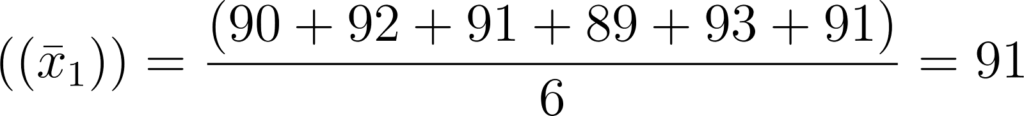
- Variância do Grupo 1:
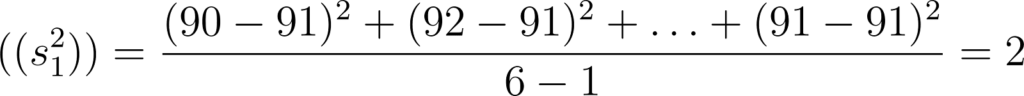
- Média do Grupo 2:

- Variância do Grupo 2:
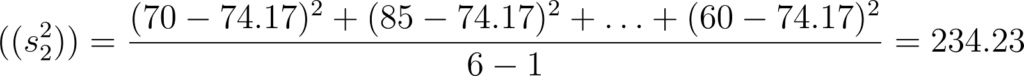
Com o desvio padrão, que é a raiz quadrada da variância, trazemos de volta a medida de original dos dados:
Desvio padrão do Grupo 1:
– Variância amostral:

– Desvio padrão amostral:
Desvio padrão do Grupo 2:
– Variância amostral:
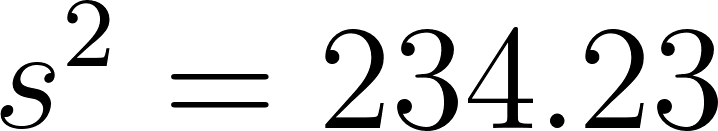
Interpretação dos resultados deste exemplo:
– Desvio padrão amostral:
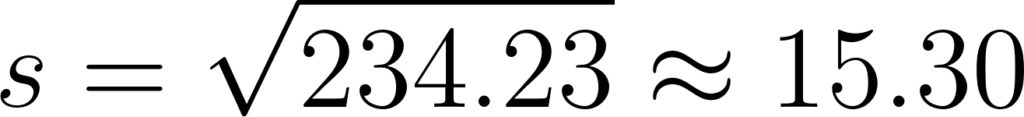
*arredondado para duas casas decimais os respectivos desvios
A variância e o desvio padrão do Grupo 2 são maiores que os do Grupo 1, indicando que as notas dos estudantes no Grupo 2 estão mais dispersas em relação à média, ou seja, há uma maior variabilidade nas notas do Grupo 2. O desvio padrão, sendo a raiz quadrada da variância, é mais facilmente interpretável pois está na mesma unidade que os dados originais (neste caso, pontos em um teste). Portanto, enquanto a variância do Grupo 2 é 234, 23 pontos, o desvio padrão é 15,30 pontos, o que faz sentido intuitivo ao comparar a dispersão dos dados.
Correlação (ρ ou r):
A correlação, que mede a força e a direção da associação entre duas variáveis, foi formalizada por Karl Pearson no final do século XIX e início do século XX. A notação ρ (para uma população) e r (para uma amostra) é agora padrão na literatura estatística.
A correlação é uma técnica estatística utilizada para entender a relação entre duas ou mais variáveis. Em termos simples, ela ajuda a verificar como uma variável muda ou se move em relação a outra. Isso é especialmente útil em muitos campos como psicologia, medicina, ciência social, e em negócios para tomar decisões informadas.
Por exemplo, suponhamos que você queira saber se existe uma relação entre as horas estudadas e as notas obtidas pelos estudantes. Se a correlação for alta, isso pode indicar que quanto mais horas os estudantes estudam, melhores notas eles obtêm.
Distribuições (N, B, P, t, F):
As distribuições são conceitos centrais na estatística que descrevem como os valores de uma variável estão distribuídos ou espalhados. Cada distribuição tem propriedades e características únicas que podem ser descritas usando parâmetros como a média (μ) e o desvio padrão (σ). Vários símbolos estatísticos e notações foram desenvolvidos para descrever diferentes tipos de distribuições. Algumas das distribuições mais comuns incluem a Distribuição Normal(N), a Distribuição Binomial(B), a Distribuição de Poisson(P), t de Student (t), e F de Fisher (F) cada uma com suas próprias notações e fórmulas associadas.
As distribuições estatísticas surgiram ao longo dos séculos como resultado da evolução da teoria da probabilidade e da análise estatística. Aqui estão alguns marcos históricos significativos e descobertas relacionadas a distribuições específicas, juntamente com as fontes correspondentes:
Distribuição Normal:
A Distribuição Normal ou Gaussiana, também conhecida como curva de sino, é uma distribuição estatística que tem uma forma de sino simétrica. Nesta distribuição, a maioria dos dados cai perto da média (o pico do sino), e poucos valores são encontrados longe da média nas caudas. É uma distribuição comum na natureza e é frequentemente usada em estatística e ciência para entender e analisar dados variáveis.
- Século XVIII: Abraham de Moivre, notou que a distribuição binomial se aproximava de uma curva suave à medida que o número de eventos aumentava, o que levou à descoberta da “curva normal”.
- 1778: Laplace descobriu a distribuição normal ao derivar o Teorema do Limite Central, mostrando que a distribuição das médias de amostras repetidas seria muito próxima da normal, independentemente da distribuição original.
O Teorema do Limite Central é uma regra que diz que, se você pegar muitas amostras de um grupo e calcular a média de cada amostra, então a distribuição dessas médias será normalmente distribuída.
- 1808-1809: Adrain e Gauss desenvolveram independentemente a fórmula para a distribuição normal, encontrando uma aplicação significativa na análise de erros de medição em observações astronômicas.
Distribuição Binomial:
A Distribuição Binomial ajuda a identificar a probabilidade de um resultado específico ocorrer, com base em dados previamente verificados. Ela é utilizada para analisar situações onde existem apenas dois possíveis resultados: sucesso ou fracasso, em uma sequência de tentativas independentes.
- 1713: Jakob Bernoulli descobriu a distribuição binomial em seu trabalho “Ars Conjectandi”.
- Inicialmente estudada em jogos de pura chance, a distribuição binomial foi utilizada para modelar o número de sucessos em uma série de tentativas independentes.
- A evolução da distribuição binomial foi influenciada por estudos de contagem de casos na antiga Índia e Grécia, bem como pela formalização de padrões numéricos ao longo do tempo, destacando a longa história e a evolução gradual dessa distribuição.
Distribuição de Poisson:
A Distribuição de Poisson é uma distribuição de probabilidade discreta que descreve a ocorrência de eventos em um intervalo de tempo ou espaço fixo, quando estes eventos ocorrem de maneira independente e em uma taxa média constante. Essa distribuição é frequentemente utilizada quando a probabilidade de um evento ocorrer é baixa, mas o número de tentativas ou o tamanho da amostra é grande. Por exemplo, pode ser usado para modelar o número de chamadas recebidas em uma central telefônica em um determinado período de tempo, ou o número de falhas em um sistema ao longo de um período específico.
Na estatística, o termo "discreta" refere-se a um tipo específico de variável ou distribuição. Uma variável discreta é aquela que pode assumir apenas valores específicos e distintos, geralmente contáveis, em um determinado intervalo. Cada valor distinto que a variável discreta pode assumir é separado por um intervalo no qual nenhum valor é possível. Em outras palavras, variáveis discretas podem assumir valores que são contáveis, como 0, 1, 2, 3, e assim por diante, mas não podem assumir valores contínuos ou fracionários. Por exemplo, o número de carros em uma garagem, o número de alunos em uma sala de aula, ou o número de vezes que um evento ocorre em um intervalo específico (como na Distribuição de Poisson) são exemplos de variáveis discretas. Você pode ter 3 carros, 4 carros, ou 5 carros em uma garagem, mas você não pode ter 3.5 carros.
Na Distribuição de Poisson, a variável aleatória X representa o número de vezes que um evento ocorre em um dado intervalo. Por exemplo, se estamos interessados em contar o número de vezes que um carro passa por um ponto específico em uma hora, X seria o número de carros que passam nesse ponto durante essa hora.
1837: Siméon Denis Poisson introduziu a distribuição de Poisson em seu trabalho sobre a teoria da probabilidade, particularmente focado na análise de convicções errôneas em matérias criminais e civis.
Distribuição t de Student:
A Distribuição t de Student serve para estimar a média de uma população baseada em uma amostra pequena ou quando o desvio padrão da população é desconhecido. Ou seja, A Distribuição t de Student é uma distribuição de probabilidade que se manifesta naturalmente ao tentar determinar a média de uma população (que segue a distribuição normal) a partir de uma amostra. Nesses problemas, não se sabe a média ou o desvio padrão da população, mas assume-se que a população segue uma distribuição normal.
1908: A distribuição t foi introduzida por William Sealy Gosset sob o pseudônimo de Student. Gosset trabalhava para a cervejaria Guinness e desenvolveu a distribuição t para lidar com pequenas amostras devido às restrições de custo na obtenção de dados.
Distribuição F de Fisher:
A Distribuição F de Fisher, também conhecida como distribuição Fisher-Snedecor, é uma distribuição de probabilidade contínua que é frequentemente utilizada em testes de hipóteses e análise de variância (ANOVA). Geralmente, é utilizada para comparar a variabilidade de duas amostras de população ou para determinar se as variâncias de duas populações são iguais. Por exemplo, suponha que você tenha as notas de dois diferentes grupos de estudantes em um exame. Se você quiser verificar se há uma diferença significativa na variação das notas entre os dois grupos, a Distribuição F pode ser utilizada.
A probabilidade contínua é um conceito que se aplica a eventos onde as variáveis aleatórias podem assumir valores em um intervalo contínuo (não discreto). Em outras palavras, ao contrário das distribuições discretas onde as variáveis aleatórias podem assumir valores separados e distintos, nas distribuições contínuas as variáveis podem assumir qualquer valor dentro de um intervalo específico. Este intervalo pode ser finito ou infinito. Para ilustrar, considere a altura de um grupo de pessoas. A altura é uma variável contínua, pois pode assumir qualquer valor dentro de um intervalo específico (por exemplo, entre 1,5 metros e 2 metros). Não há lacunas nos valores possíveis que a altura pode assumir neste intervalo.
- 1922: A forma da distribuição F foi dada por Sir Ronald Fisher, sendo às vezes ainda referida como distribuição F de Fisher..
- 1934: A distribuição foi tabulada por Snedecor, que usou a letra F em homenagem a Fisher.
- A distribuição F foi desenvolvida por Fisher para estudar o comportamento de duas variâncias de amostras aleatórias retiradas de duas populações normais independentes.
Estes são apenas alguns exemplos do surgimento e evolução de distribuições estatísticas, indicando que o desenvolvimento de distribuições e notações associadas foi um processo cumulativo que se estendeu por vários séculos, com contribuições significativas de vários matemáticos e estatísticos ao longo do tempo. As distribuições estatísticas têm sido fundamentais para a compreensão e análise de fenômenos naturais e sociais, e continuam sendo uma parte essencial da ciência de dados, aprendizado de máquina e muitos outros campos da ciência e engenharia.
Entenda a filosofia por trás das Distribuições
Para muitos, há uma certa dificuldade em entender a filosofia por trás das distribuições. Como você pode perceber são várias as formas de análise, mas no final das contas, uma distribuição é uma forma de organizar ou representar dados, mostrando a frequência com que diferentes valores ocorrem.
Vamos contextualizar, Imagine que você tenha um grande número de dados, como as notas de todos os alunos em uma sala de aula. Uma distribuição te ajuda a entender como essas notas estão espalhadas: há muitos alunos com notas altas? As notas estão concentradas em torno de uma média? Ou as notas estão espalhadas igualmente através da escala de avaliação?
As distribuições estatísticas, quando compreendidas e aplicadas corretamente, podem fornecer insights significativos, melhorar a precisão dos modelos, e auxiliar na tomada de decisões informadas em muitas áreas da tecnologia e da ciência de dados.
Nas referências você encontrará diversas fontes ricas em conhecimento que podem lhe ajudar a se aprofundar enormemente nesta jornada no que tange aspectos estatísticos. Não se esqueça de compartilhar este artigo nas suas redes para mostrar aos possíveis parceiros profissionais, qual é a sua busca por conhecimento e evolução profissional. Até o próximo artigo!
Confiança Sempre!!!
Referências:
- BRITANNICA. Probability and statistics | History, Examples, & Facts. Disponível em: https://www.britannica.com/science/probability. Acesso em: 27 out. 2023.
- WIKIPEDIA. History of statistics. Disponível em: https://en.wikipedia.org/wiki/History_of_statistics.
- Stigler, S. M. (1986). The history of statistics: The measurement of uncertainty before 1900. Harvard University Press.
- Pearson, K. (1920). Notes on the history of correlation. Biometrika, 13(1), 25-45.
- Hald, A. (1998). A history of mathematical statistics from 1750 to 1930. Wiley Series in Probability and Statistics.
- Galton, F. (1889). Natural Inheritance. MacMillan and Co.
- Fienberg, S. E. (2006). When did Bayesian inference become “Bayesian”? Bayesian Analysis, 1(1), 1-40.
- BRITANNICA. Probability and Statistics. Disponível em: https://www.britannica.com/science/probability. Acesso em: 27 out. 2023.
- ITFEATURE.COM. A Short History of Statistics – Basic Statistics and Data Analysis. Disponível em: https://itfeature.com/statistics/a-short-history-of-statistics. Acesso em: 27 out. 2023.
- SPRINGERLINK. Binomial Distribution. Disponível em: https://link.springer.com/referenceworkentry/10.1007%2F978-1-4614-1564-8_101. Acesso em: 28 out. 2023.
- BRITANNICA. Binomial distribution | Probability, Statistics & Mathematics. Disponível em: https://www.britannica.com/science/binomial-distribution. Acesso em: 28 out. 2023.
- MDPI. The Binomial Distribution: Historical Origin and Evolution of Its. Disponível em: https://www.mdpi.com/2227-7390/9/1/89. Acesso em: 28 out. 2023.
- WIKIPEDIA. History of statistics. Disponível em: https://en.wikipedia.org/wiki/History_of_statistics. Acesso em: 28 out. 20234.
- STATISTICS LIBRETEXTS. 7.2: History of the Normal Distribution. Disponível em: https://stats.libretexts.org/Bookshelves/Introductory_Statistics/Book%3A_Introductory_Statistics_(Shafer_and_Zhang)/07%3A_The_Normal_Distribution/7.02%3A_History_of_the_Normal_Distribution. Acesso em: 28 out. 2023.
- SPRINGER. William Sealy Gosset, 1876–1937. Disponível em: https://link.springer.com/chapter/10.1007/978-1-4471-3677-9_6. Acesso em: 28 out. 2023.
- STATISTICAL SCIENCE. Student: A Statistical Biography of William Sealy Gosset. Disponível em: https://projecteuclid.org/euclid.ss/1177011576. Acesso em: 28 out. 20238.
- AMERICAN STATISTICIAN. “Student’s” t Distribution: The Teaching of Statistics. Disponível em: https://www.tandfonline.com/doi/abs/10.1080/00031305.1977.10479237. Acesso em: 28 out. 20239.
- JSTOR. Studies in the History of Probability and Statistics. XXV. On the. Disponível em: https://www.jstor.org/stable/2985170. Acesso em: 28 out. 202310.
- OXFORD REFERENCE. F-distribution. Disponível em: www.oxfordreference.com. Acesso em: 28 out. 2023
- SCIENCE DIRECT. F-Distribution. Disponível em: https://www.sciencedirect.com/topics/mathematics/f-distribution. Acesso em: 28 out. 2023
- WIKIPEDIA. F-distribution. Disponível em: https://en.wikipedia.org/wiki/F-distribution. Acesso em: 28 out. 2023
- LABONE CONSULTORIA. Distribuição Binomial: Entenda o que é e como fazer. Disponível em: https://www.laboneconsultoria.com.br/distribuicao-binomial/. Acesso em: 27 out. 2023.
- PROFESSOR GURU. Distribuição Binomial. Disponível em: https://www.professorguru.com.br/distribuicao-binomial. Acesso em: 28 out. 2023.
- VOITTO. Distribuição Binomial: aprenda o que é e como fazer! Disponível em: https://www.voitto.com.br/distribuicao-binominal-aprenda-o-que-e-e-como-fazer. Acesso em: 28 out. 2023.
- ESTUDYANDO. Distribuição Binomial: Definição, Fórmula e Exemplos. Disponível em: https://pt.estudyando.com/distribuicao-binomial-definicao-formula-e-exemplos. Acesso em: 28 out. 2023.
- ESCOLA EDTI. Utilizando a Distribuição Binomial e Suas Probabilidades. Disponível em: https://www.escolaedti.com.br/utilizando-a-distribuicao-binomial-e-suas-probabilidades. Acesso em: 28 out. 2023.
- VOITTO. Distribuição Poisson: o que é, como calcular e exemplos práticos. Disponível em: https://www.voitto.com.br/blog/artigo/distribuicao-poisson. Acesso em: 28 out. 2023.
- LABONE. Distribuição de Poisson. Disponível em: https://labone.info/distribuicao-de-poisson/. Acesso em: 28 out. 2023.
- PROFESSOR GURU. Distribuição de Poisson. Disponível em: https://www.professorguru.com.br/estatistica/distribuicao-de-poisson. Acesso em: 28 out. 2023.
- BLOG DA PROF. FERNANDA MACIEL. Distribuição de Poisson. Disponível em: https://blog.proffernandamaciel.com.br/distribuicao-de-poisson/. Acesso em: 28 out. 2023.
- MAESTRO VIRTUALE. Distribuição de Poisson. Disponível em: https://maestrovirtuale.com/distribuicao-de-poisson/. Acesso em: 28 out. 2023.
- SWEET. “A distribuição t de Student”. Disponível em: https://sweet.ua.pt/pedrocruz/bioestatistica/da-t.html. Acesso em: 29 out. 2023.
- PROFES. “O que é distribuição t de Student?”. Disponível em: https://profes.com.br . Acesso em: 29 out. 2023.
- WIKIPEDIA. “Distribuição t de Student”. Disponível em: https://pt.wikipedia.org/wiki/Distribui%C3%A7%C3%A3o_t_de_Student . Acesso em: 29 out. 2023.
- CENTRO DE ESTATÍSTICA APLICADA. “t de Student”. Disponível em: http://estatistica.pt . Acesso em: 29 out. 2023.
- ESTUDYANDO. “Distribuição t do aluno: definição e exemplo”. Disponível em: https://pt.estudyando.com . Acesso em: 29 out. 2023.
- QUALITY GURUS. F-distribution. Disponível em: https://www.qualitygurus.com/f-distribution/. Acesso em: 29 out. 2023.
- WIKIPEDIA. F-distribution. Disponível em: https://en.wikipedia.org/wiki/F-distribution. Acesso em: 29 out. 2023.
- WIKIPEDIA (Português). Distribuição F de Fisher-Snedecor. Disponível em: https://pt.wikipedia.org/wiki/Distribui%C3%A7%C3%A3o_F_de_Fisher-Snedecor. Acesso em: 29 out. 2023.
- SPRINGERLINK. F Distribution. Disponível em: https://link.springer.com/referenceworkentry/10.1007%2F978-3-540-38990-7_152. Acesso em: 29 out. 2023.
- OXFORD REFERENCE. F-distribution. Disponível em: https://www.oxfordreference.com/view/10.1093/oi/authority.20110803095811586. Acesso em: 29 out. 2023.



Seja o primeiro a comentar