Explorando Médias Estatísticas: Uma Jornada Profunda na Matemática por Trás da Ciência de Dados e Machine Learning

Atualizado pela última vez em 1 de novembro de 2023

A matemática, muitas vezes vista como a linguagem universal, tem suas raízes fincadas profundamente na história da humanidade. Dentre seus ramos, a estatística se destaca como uma ferramenta crucial na compreensão e interpretação de conjuntos de dados. Um conceito fundamental neste domínio é o cálculo das médias, que permite aos pesquisadores resumir uma série de valores num único valor representativo. Este artigo propõe um mergulho na evolução histórica e na lógica subjacente dos diferentes tipos de média: a média aritmética, a média geométrica e a média harmônica.

O entendimento profundo e a exploração do conceito de média é fundamental em diversos campos, incluindo ciência de dados e aprendizado de máquina. Vamos explorar cada uma dessas métricas, seu contexto histórico e a lógica subjacente que as fundamenta.

Média Aritmética:

A média aritmética, provavelmente a mais comum entre as médias, tem sido utilizada desde os tempos antigos. Os pitagóricos e matemáticos gregos subsequentes já exploravam o conceito básico de média aritmética devido à sua importância em geometria e música. No entanto, a notação moderna usando  x̅ (para uma amostra; “x barra”) e μ (para uma população; pronuncia-se “mi”) se tornou comum a partir do século XIX, coincidindo com o advento da teoria da probabilidade e da estatística moderna​.

Basicamente, a média aritmética é a soma de todos os valores de um conjunto de dados dividido pelo número de valores no conjunto. É uma medida de centralidade que fornece um valor representativo para o conjunto de dados.

A média populacional é a média de todos os valores em uma população. A fórmula para a média populacional (μμ) é:

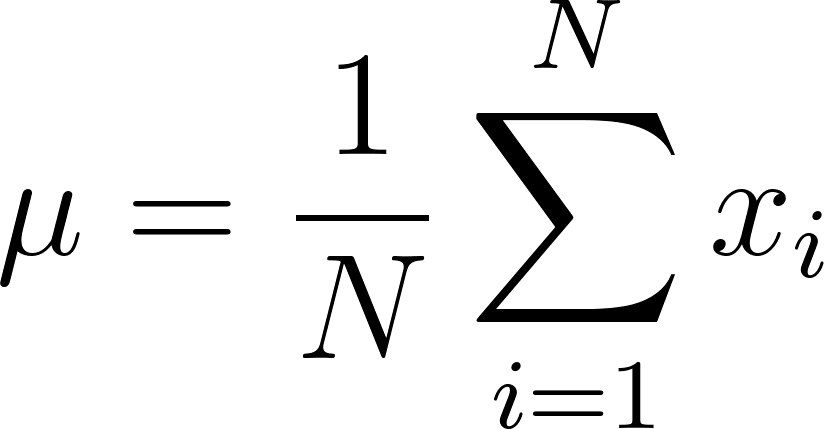
onde:

• N é o número total de valores na população,
• x_i​ são os valores individuais na população,
• μ é a média populacional.

A média amostral é a média de todos os valores em uma amostra. A fórmula para a média amostral (x̅) é:

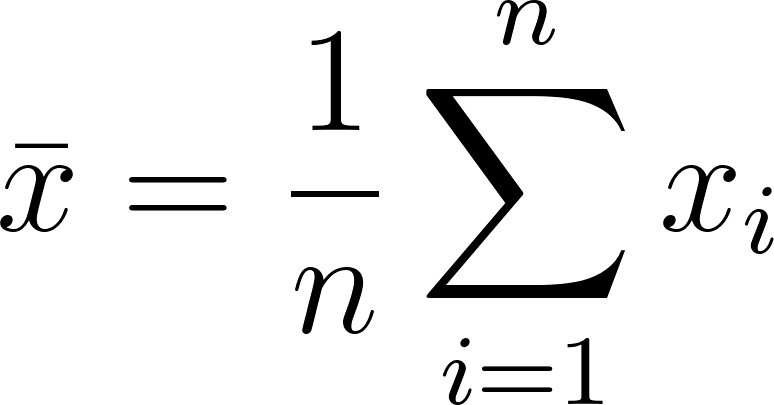
onde:

• n é o número total de valores na amostra,
• x_i​ são os valores individuais na amostra,
• x̅ é a média amostral.

Ambas as fórmulas são bastante semelhantes em estrutura, com a principal diferença sendo o tamanho do conjunto de dados sendo considerado – a população total versus uma amostra da população. Isso é crucial para garantir uma análise estatística precisa, pois a média amostral é uma estimativa da média populacional, e o tamanho da amostra pode influenciar a precisão dessa estimativa.

Caso você não se recorde como funciona o somatório (Σ), o somatório é a adição de uma sequência de números. É representado pelo símbolo Σ (a letra grega maiúscula Sigma). Por exemplo, se temos um conjunto de números x={1,2,3,4}, o somatório de x é 1+2+3+4 = 10.

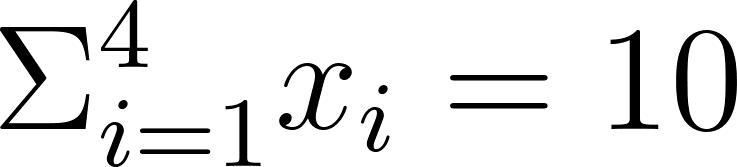
Outro conceito importante para recordar é o uso de frações, como no caso da fórmula da média aritmética onde tem um 1/n na frente do somatório. Esse 1/n​ representa a operação de divisão pelo número total de elementos no conjunto de dados, onde n é o número de elementos.

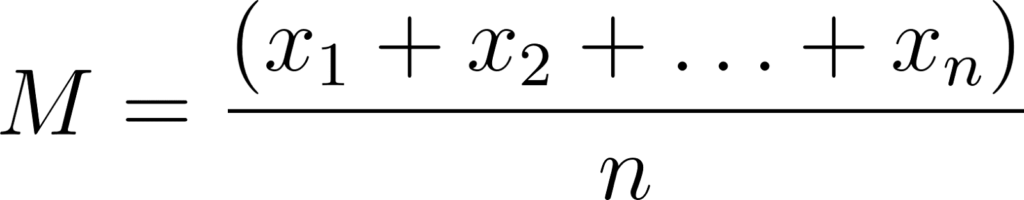
Na prática, usando em combinação com o somatório, encapsulamos essa expressão para facilitar a leitura:

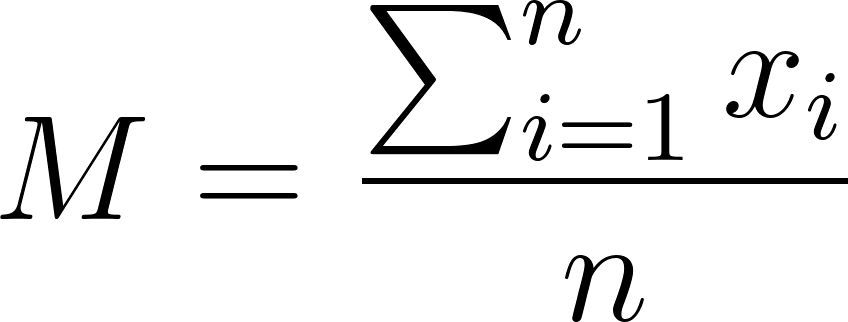
Revisão feita, continuando sobre as médias. A literatura apresenta várias variações e usos da média aritmética para lidar com diferentes cenários ou dados com características particulares. Algumas dessas variações incluem:

Média Aritmética Ponderada:

A Média Aritmética Ponderada (MPA) é uma extensão da média aritmética simples que permite dar diferentes pesos a diferentes valores em um conjunto de dados. Essa variação é particularmente útil em situações onde alguns valores têm mais importância ou relevância do que outros.. A fórmula para a média aritmética ponderada é:

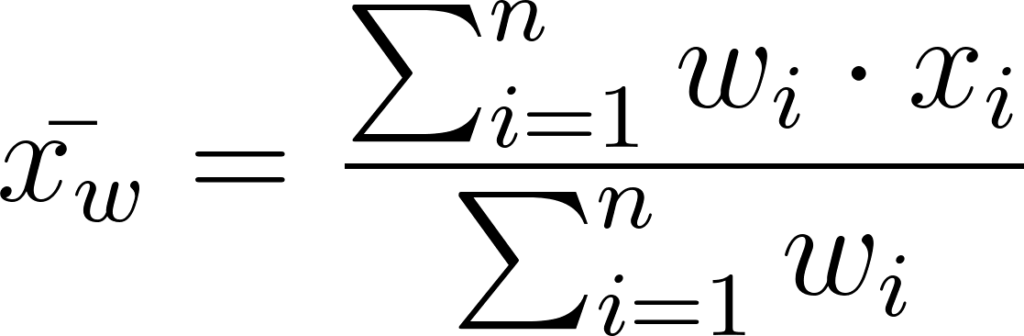
onde:

• n é o número total de valores no conjunto,
• x_i​ são os valores individuais no conjunto,
• w_i​ são os pesos associados a cada valor xixi​,
• x̅ é a média aritmética ponderada.

Imagine que você tem uma sacola de maçãs e peras, e você quer encontrar uma “média de frutas” na sua sacola. No entanto, você gosta mais de maçãs do que de peras. Então, você decide que as maçãs vão contar um pouco mais na sua “média de frutas”.

Aqui é onde os “pesos” entram. Os pesos são como pontos extras que você dá para as coisas que são mais importantes para você. No nosso exemplo, você daria mais pontos (ou um peso maior) para as maçãs do que para as peras, porque você gosta mais delas.

Agora, vamos traduzir isso para números. Suponha que você tenha 3 maçãs e 2 peras. Se todas as frutas fossem igualmente importantes para você, a média seria simplesmente (3+2) / 2 = 2.5. Mas como você gosta mais de maçãs, você decide dar a elas um peso de 2 e às peras um peso de 1.

Agora, a conta fica assim:

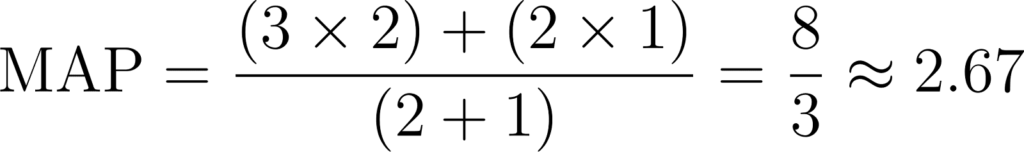
Então, mesmo que você tenha mais maçãs do que peras, a média ponderada é um pouco maior porque você deu mais “peso” ou importância às maçãs.

Essa é a ideia por trás dos pesos na média aritmética ponderada. Eles são uma maneira de dizer “isso é mais importante para mim” ao fazer a média.

A  MAP é frequentemente utilizada para calcular a nota final de estudantes em cursos que têm diferentes atividades avaliativas com pesos diferentes, como provas, trabalhos, apresentações, etc. Também você encontrará seu uso em cálculo de índices de preços, como o Índice de Preços ao Consumidor, onde diferentes bens e serviços têm pesos diferentes baseados na quantidade que os consumidores compram de cada um.

Média Quadrática:

A Média Quadrática (MQ), também conhecida como Raiz Quadrada da Média dos Quadrados (RMS, do inglês Root Mean Square), é uma medida estatística que é frequentemente usada quando se deseja representar a magnitude de um conjunto de números, ignorando a direção (positivo ou negativo) desses números. Ou seja, é especialmente útil em situações onde os valores podem ser tanto positivos quanto negativos, e você está mais interessado na magnitude (tamanho) dos valores do que na sua direção. A fórmula para a média quadrática é dada por:

onde:

• n é o número total de valores no conjunto,
• x_i​ são os valores individuais no conjunto,
• M_q é a média quadrática.

Imagine que você está jogando dardos com seus amigos, e todos vocês estão tentando acertar o centro do alvo. Após cada rodada, vocês medem a distância de cada dardo até o centro do alvo. Você quer encontrar uma maneira de descrever o quão bem ou mal cada um está jogando, considerando todas as rodadas.

Vamos supor que vocês jogaram três rodadas, e estas foram as distâncias dos seus dardos ao centro do alvo em cada rodada: 2 cm, 4 cm e 6 cm.

Se você simplesmente tirar a média aritmética dessas distâncias, você somaria as distâncias e dividiria pelo número de rodadas:

Média Aritmética = (2 cm + 4 cm + 6 cm) / 3 = 4 cm

Mas essa média aritmética não dá uma boa ideia da “magnitude” das suas distâncias ao alvo. Então, você decide usar a Média Quadrática.

Para calcular a MQ, primeiro, você elevaria ao quadrado cada distância, depois, encontraria a média desses quadrados, e finalmente, tiraria a raiz quadrada dessa média:

1. Quadrado de cada distância: 2²=4, 4²=16, 6²= 36
2. Média dos quadrados: ( 4 + 16 + 36 ) / 3 = 18.67
3. Raiz quadrada da média dos quadrados: 

Então, a MQ das suas distâncias ao centro do alvo é aproximadamente 4,32 cm. Este valor é um pouco maior do que a média aritmética, refletindo o fato de que houve uma distância maior de 6 cm na última rodada. A MQ dá mais “peso” às distâncias maiores, fornecendo uma ideia melhor da variação nas suas jogadas.

A MQ é frequentemente utilizada na análise de sinais elétricos ou de áudio, pois fornece uma medida da magnitude do sinal, independentemente da direção em que o sinal varia; Em acústica, a MQ é usada para calcular níveis de pressão sonora, que podem variar acima e abaixo de um valor médio. Enfim, a escolha de usar a MQ depende da natureza dos dados e do contexto da análise. 

Média Truncada:

A Média Truncada(MT) ou Média Aparada,  é uma variação da média aritmética tradicional, que busca eliminar a influência de valores extremos (outliers) no cálculo da média. Esta média é especialmente útil em situações onde os dados podem conter valores anormalmente altos ou baixos que podem distorcer a média. 

Aqui está a fórmula geral para a média truncada de um conjunto de dados x₁,x₂,…,x_n​ após truncar uma porcentagem p das observações (ou seja, p/2% das observações de cada extremidade):

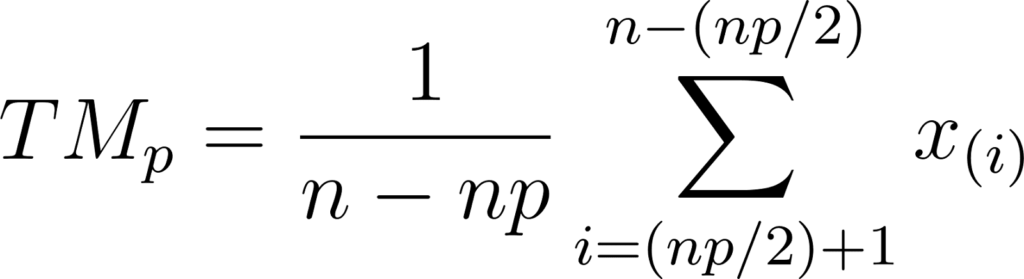
onde:

• TM_p​ é a média truncada,
• n é o número total de observações,
• p é a porcentagem de observações a ser truncada (e.g., p=0.20 para truncar 20% das observações),
• x_(i)​ são os valores das observações ordenadas em ordem crescente,
• A soma é calculada sobre as observações restantes após o truncamento.

Na prática, a MT é calculada da seguinte maneira:

1. Os valores da amostra ou da distribuição são ordenados.
2. Uma certa porcentagem ou um número fixo de valores nas extremidades superior e inferior é removido.
3. A média aritmética dos valores restantes é calculada.

Por exemplo, para uma amostra de 8 pontos, se 12,5% dos dados forem truncados, os valores mínimo e máximo serão descartados, e a média será então calculada com os 6 pontos restantes.

A mediana pode ser vista como uma média totalmente truncada e é a mais robusta. Uma das principais vantagens da média truncada é sua robustez e maior eficiência para distribuições mistas e distribuições de caudas pesadas, como a distribuição de Cauchy. A remoção de valores extremos ajuda a obter uma estimativa mais precisa da tendência central, especialmente quando os outliers podem distorcer significativamente a média aritmética simples​​.

Em algumas regiões da Europa Central, a MT é também conhecida como a média de Windsor, embora essa denominação possa ser confundida com a média Winsorizada, onde os valores que seriam descartados são substituídos pelos maiores/menores dos valores restantes​.

A MT é particularmente benéfica em situações onde é crucial obter uma estimativa de tendência central que seja resistente a outliers. Um exemplo prático é o uso em julgamentos olímpicos, onde a média truncada evita que um único juiz altere significativamente a pontuação geral ao dar uma pontuação excepcionalmente alta ou baixa​.

Média Geométrica:

A Média Geométrica (MG) é uma forma de calcular a tendência central de um conjunto de dados, semelhante à Média Aritmética, mas com uma abordagem diferente. Enquanto a média aritmética simplesmente soma todos os valores e divide pelo número de valores, a MG multiplica todos os valores juntos e depois tira a raiz n-ésima do resultado, onde n é o número de valores no conjunto de dados. A fórmula para a média geométrica é:

A expressão 1/n na fórmula da média geométrica serve para indicar que estamos tirando uma raiz do produto dos números, e o n nos diz que tipo de raiz estamos tirando.

Quando queremos tirar a raiz quadrada de um número, estamos basicamente perguntando “qual número, multiplicado por si mesmo, dá esse número?”. Por exemplo, a raiz quadrada de 9 é 3 porque 3 × 3 = 9.

Como você sabe, a notação matemática para a raiz quadrada é √ ou, de forma equivalente, elevar o número a 1/2 (meio). Por exemplo, 9 = 9^1/2 =3. No caso desta fórmula, o que vai definir qual o tipo de raiz, vai ser n. Supondo n = 3, então teríamos algo como,   de forma equivalente, elevar o número a 1/3 (um terço). Teríamos, por exemplo, 27^1/3=3, que é  o mesmo que raiz cúbica de 27.

Esta fórmula pode ser representada também utilizando o símbolo do produtório ∏ (a letra grega maiúscula Pi), que representa a multiplicação de todos os valores em um conjunto ou sequência:

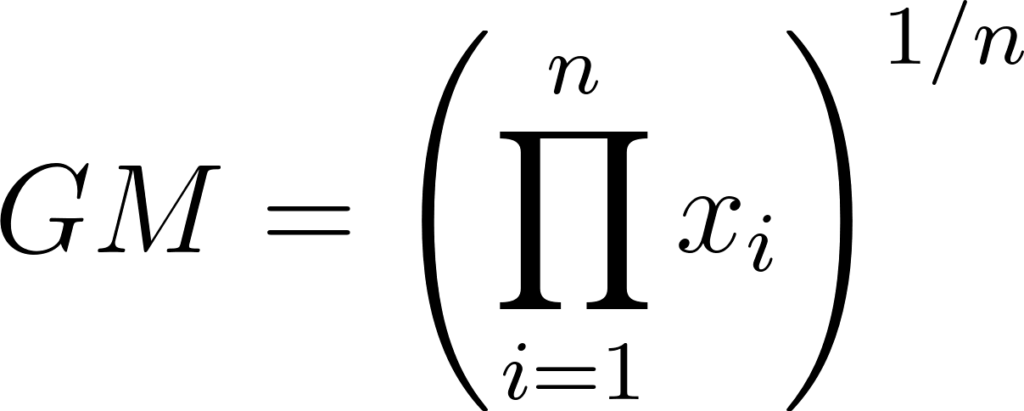
onde:

• x_i​ são os valores no conjunto de dados,
• n é o número de valores no conjunto de dados,
• ∏ denota a multiplicação de todos os valores x_i​ no conjunto de dados.

Só para relembrar o conceito, usando o conjunto de números x={1,2,3,4}, o produtório de x é 1×2×3×4 = 24

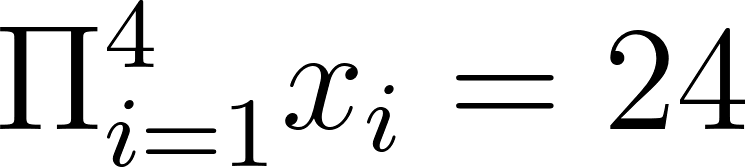
A Média Geométrica é especialmente útil em situações que envolvem multiplicação ou crescimento exponencial de valores. Aqui estão alguns cenários comuns onde a média geométrica pode ser aplicada:

• Quando você tem várias taxas de crescimento percentual (como taxas de retorno anuais de um investimento);
• Para calcular o retorno composto de investimentos ao longo do tempo;
• na construção de índices de preços e índices de mercado, como o índice de preço ao consumidor ou índices de ações, para refletir as mudanças percentuais de preços ao longo do tempo;
• Ao avaliar o desempenho de produtos com múltiplas dimensões ou características;

Estas são apenas algumas das suas aplicações. Ao final deste artigo, você encontrará referências caso você queira se aprofundar um pouco mais.

Média Harmônica:

A Média Harmônica(MH) tem uma longa história, sendo utilizada em teoria musical e acústica desde os tempos antigos.

A MH é especialmente útil em situações onde as relações recíprocas dos valores são importantes. Este tipo de média é frequentemente encontrada em problemas de física e engenharia, como a harmonização de taxas ou velocidades. A fórmula para calcular a MH de n números é dada por:

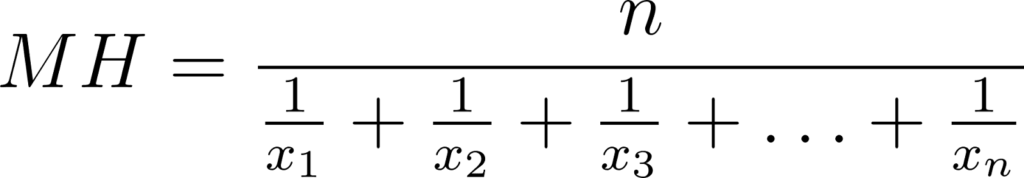
Onde n é o número de valores no conjunto, e x₁,x₂,x₃,…,x_n são os valores individuais do conjunto. Em vez de simplesmente somar todos os números e dividir pelo total de números (como na média aritmética), na média harmônica, nós:

1. Calculamos o inverso (ou recíproco) de cada número,
2. Somamos todos esses inversos,
3. Dividimos o número total de valores pela soma dos inversos.

O que é um inverso ou recíproco?

O inverso ou recíproco de um número é simplesmente 1 dividido por esse número (como você pode observar na fórmula acima). Por exemplo:

• O inverso de 2 é 1/2 = 0.5
• O inverso de 3 é 1/3 ≈ 0.333
• O inverso de 4 é 1/4 = 0.25, e assim por diante.

Vamos considerar um exemplo simples com três velocidades: 10 km/h, 20 km/h e 30 km/h.

1. Primeiro, encontramos o inverso de cada velocidade:
   • Inverso de 10 km/h é 1/10 = 0.1,
   • Inverso de 20 km/h é 1/20 = 0.05,
   • Inverso de 30 km/h é 1/30 ≈ 0.0333.
2. Agora, somamos esses inversos: 0.1 + 0.05 + 0.0333 ≈ 0.1833.
3. Finalmente, dividimos o número total de velocidades (que é 3) pela soma dos inversos: 3 / 0.1833 ≈ 16.36 km/h.

Portanto, a média harmônica das velocidades é 16.36 km/h.

Abaixo estão algumas situações comuns onde a média harmônica pode ser a escolha adequada para representar uma média:

1. Taxas de Velocidade Variáveis:

Quando um veículo viaja a diferentes velocidades sobre diferentes distâncias, a média harmônica proporciona uma representação mais precisa da velocidade média ao longo de toda a viagem​.

2. Taxas de Transferência em Redes:

Ao avaliar a performance de redes com diferentes taxas de transferência, a média harmônica pode oferecer uma visão mais acurada da taxa média de transferência.

3. Resistência em Circuitos Paralelos:

Em eletrônica, ao calcular a resistência total de resistores em paralelo, utiliza-se a média harmônica para obter a resistência equivalente.

4. Harmonização de Preços ou Taxas:

Em cenários financeiros ou econômicos, a média harmônica pode ser utilizada para harmonizar preços ou taxas que têm uma relação recíproca.

5. Avaliação de Investimentos:

Em finanças, a média harmônica pode ser usada para avaliar a performance média de investimentos ao longo do tempo, especialmente quando as taxas de retorno são variáveis.

6. Média de Razões:

Em situações onde é necessário calcular a média de razões ou proporções, a média harmônica pode ser mais representativa.

7. Média de Tempo por Unidade:

Em operações onde o tempo por unidade é uma métrica crucial, como em manufatura ou logística, a média harmônica pode oferecer uma representação mais precisa do tempo médio por unidade.

A média harmônica é uma ferramenta estatística valiosa em muitos campos, incluindo física, engenharia, matemática, economia, e finanças, oferecendo uma maneira de sintetizar um conjunto de valores em um único valor médio que reflete as relações recíprocas entre esses valores.

A escolha da métrica de média apropriada depende altamente do contexto e da natureza dos dados. Cada uma destas médias têm suas próprias propriedades, vantagens e desvantagens. A compreensão profunda de como e quando aplicar estas médias pode enriquecer a análise dos dados e proporcionar insights mais precisos e informativos.

No próximo artigo, vamos expandir nossa exploração sobre as médias, abordando outras métricas que são cruciais em Data Science e Machine Learning, além das já discutidas anteriormente. Algumas delas incluem:

1. Mediana:

A Mediana é um indicador de tendência central que separa os dados em duas metades iguais, sendo imune a outliers e, portanto, oferecendo uma representação mais robusta da tendência central dos dados.

2. Moda:

A Moda, sendo o valor mais frequente em um conjunto de dados, pode ser útil para identificar o valor mais comum em um conjunto de dados, especialmente em análises de dados categóricos.

3. Média Móvel:

Essencial para análises de séries temporais, a Média Móvel ajuda a suavizar flutuações de curto prazo e revelar tendências de longo prazo, sendo uma ferramenta vital para previsão e análise de tendências.

4. Média Winsorizada:

Semelhante à Média Truncada, mas substituindo os valores extremos em vez de removê-los, a Média Winsorizada é robusta a outliers, sendo útil em análises onde outliers podem ser problemáticos.

5. Média Média (ou Média de Médias):

Em situações onde é necessário analisar a média de várias médias aritméticas, esta métrica pode ser empregada, sendo útil quando há múltiplas amostras de diferentes populações.

6. Média Biweight:

Uma média robusta que oferece uma boa eficiência em dados normalmente distribuídos enquanto é resistente a outliers, sendo útil em análises de dados que podem conter valores extremos.

7. Média Logarítmica:

Em contextos especializados, a Média Logarítmica pode ser útil, especialmente quando os dados têm uma natureza multiplicativa ou exponencial.

8. Média Geométrica Ponderada:

Extensão da Média Geométrica, permite dar diferentes pesos a diferentes valores em um conjunto de dados, sendo útil em cenários que envolvem multiplicação ou crescimento exponencial de valores com diferentes níveis de importância.

9. Média Harmônica Ponderada:

Similar à Média Harmônica, mas com pesos associados a cada valor, sendo útil em situações onde as relações recíprocas entre os valores são importantes e esses valores têm diferentes níveis de importância.

10. Média Generalizada:

Esta é uma família de médias que inclui a média aritmética, geométrica e harmônica como casos especiais, permitindo uma exploração mais profunda das relações entre essas médias.

11. Média Interquartil:

Uma média robusta que é calculada removendo os quartis inferior e superior dos dados, sendo útil em análises robustas de dados com outliers.

Estas métricas, junto com as já discutidas, formam um conjunto robusto de ferramentas que podem ser empregadas para extrair insights valiosos de conjuntos de dados, cada uma com sua própria vantagem dependendo da natureza dos dados e do contexto da análise. Ao explorar essas métricas em profundidade, podemos descobrir mais nuances e obter uma compreensão mais rica das tendências e padrões subjacentes nos dados. Sendo indicadores cruciais de tendência central e dispersão, são fundamentais em Data Science e Machine Learning. A Média Aritmética, ao oferecer um ponto central, facilita a compreensão da distribuição dos dados, enquanto a Média Geométrica é vital ao trabalhar com taxas de crescimento e produtos de probabilidades. A Média Harmônica, por outro lado, é útil ao harmonizar taxas e velocidades variáveis, essencial em análises de performance. A Média Quadrática é frequentemente utilizada em análise de sinais, onde a magnitude é de interesse, e a Média Truncada e a Média Aritmética Ponderada são valiosas ao lidar com outliers ou diferentes relevâncias de dados. Essas médias auxiliam na construção de modelos robustos e na extração de insights significativos dos dados em ambas as áreas, além de contribuírem para a otimização de algoritmos e a avaliação precisa de desempenho dos modelos de Machine Learning.

Se você está gostando desse conteúdo, não se deixe de deixar o seu comentário e compartilhar nas suas redes para que outros possam se beneficiar deste conteúdo que foi feito com muito zelo. Nos vemos no próximo!

Confiança Sempre!!!

Referências:

• WALL STREET MOJO. Types of Mean. Disponível em: https://www.wallstreetmojo.com/mean  Acesso em: 26 out. 2023​1​.
• RESEARCHGATE. What Does It “Mean”? A Review of Interpreting. Disponível em: https://www.researchgate.net/publication/316988215_What_Does_It_Mean_A_Review_of_Interpreting  Acesso em: 26 out. 2023​2​.
• NATIONAL CENTER FOR BIOTECHNOLOGY INFORMATION. Measures of central tendency: The mean. Disponível em: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6293379  Acesso em: 26 out. 2023​​.
• SCRIBBR. What are the different types of means? Disponível em: https://www.scribbr.com/statistics/types-of-means  Acesso em: 29 out. 2023​​.
• WIKIPEDIA. Weighted arithmetic mean. Disponível em: https://en.wikipedia.org/wiki/Weighted_arithmetic_mean . Acesso em: 27 out. 2023​​.
• WIKIPEDIA. Root mean square. Disponível em: https://en.wikipedia.org/wiki/Root_mean_square . Acesso em: 27 out. 2023​​.
• WIKIPEDIA. Generalized mean. Disponível em: https://en.wikipedia.org/wiki/Generalized_mean . Acesso em: 27 out. 2023​​.
• WIKIPEDIA. Geometric mean. Disponível em: https://en.wikipedia.org/wiki/Geometric_mean . Acesso em: 27 out. 2023​​.
• WIKIPEDIA. Harmonic mean. Disponível em: https://en.wikipedia.org/wiki/Harmonic_mean . Acesso em: 27 out. 2023​​.
• BRASIL ESCOLA. Média Harmônica. Disponível em: https://brasilescola.uol.com.br/matematica/media-harmonica.htm Acesso em: 28 out. 2023​.
• MUNDO EDUCAÇÃO. Média harmônica: o que é, fórmula, quando usar. Disponível em: https://mundoeducacao.uol.com.br/matematica/media-harmonica.htm Acesso em: 28 out. 2023​.
• INFO ESCOLA. Médias (aritmética, geométrica, harmônica) – Matemática. Disponível em: https://www.infoescola.com/matematica/medias-aritmetica-geometrica-harmonica/ Acesso em: 28 out. 2023​³​.
• MATEMÁTICA DIDÁTICA. Média Harmônica. Disponível em: https://www.matematicadidatica.com.br/MediaHarmonica.aspx Acesso em: 28 out. 2023​.
• WOLFRAM MATHWORLD. Weighted Quadratic Mean. Disponível em: http://mathworld.wolfram.com/WeightedQuadraticMean.html . Acesso em: 29 out. 2023​​.
• NATIONAL CENTER FOR BIOTECHNOLOGY INFORMATION. Different Types of Mean. Disponível em: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6293379 . Acesso em: 30 out. 2023​.
• SPRINGERLINK. Arithmetic Mean. Disponível em: https://link.springer.com/referenceworkentry/10.1007%2F978-1-4419-9863-7_117. Acesso em: 30 out. 2023​​.
• SCIENCEDIRECT. The precision of the arithmetic mean, geometric mean and percentiles. Disponível em: https://www.sciencedirect.com/science/article/abs/pii/S0167947312003568. Acesso em: 30 out. 2023​​.
• SCIENCEDIRECT. Arithmetic Mean – an overview. Disponível em: https://www.sciencedirect.com/topics/engineering/arithmetic-mean. Acesso em: 30 out. 2023​.
• TANDFONLINE. Mean, Median and Mode from a Decision Perspective. Disponível em: https://www.tandfonline.com/doi/full/10.1080/23322039.2015.1045211. Acesso em: 30 out. 2023​.
• SCIENCE DIRECT. Truncated means and variances. Disponível em: https://www.sciencedirect.com/science/article/abs/pii/S0167715219303100. Acesso em: 29 out. 2023​.
• HANDWIKI. Truncated mean. Disponível em: https://handwiki.org/wiki/Truncated_mean. Acesso em: 29 out. 2023​.
• ANDRADE, Cláudia Sá Malbouisson; TIRYAKI, Gisele Ferreira. Econometria na prática. Alta Books Editora, 2019.
• HOFFMANN, Rodolfo. Estatística para economistas. 4ª. Edição revisada e ampliada. São Paulo, 2006.
• CASELLA, George; BERGER, Roger L. Inferência estatística-tradução da 2ª edição norteamericana. Centage Learning, 2011.
• BRUCE, Andrew; BRUCE, Peter. Estatística Prática para Cientistas de Dados. Alta Books, 2019.
• CUEMATH. Geometric Mean – Definition, Examples, Applications. Disponível em: https://www.cuemath.com/algebra/geometric-mean/. Acesso em: 29 out. 2023.
• WIKIPEDIA. Geometric mean. Disponível em: https://en.wikipedia.org/wiki/Geometric_mean. Acesso em: 29 out. 2023​2​.
• EMBIBE. Geometric Mean Formula. Disponível em: https://www.embibe.com/exams/geometric-mean-formula/. Acesso em: 29 out. 2023​.
• STATISTICS BY JIM. Arithmetic, Geometric, and Harmonic Means. Disponível em: https://statisticsbyjim.com/basics/arithmetic-geometric-harmonic-means/. Acesso em: 29 out. 2023​.
• SCRIBBR. Geometric Mean. Disponível em: https://www.scribbr.com/statistics/geometric-mean/. Acesso em: 29 out. 2023​.